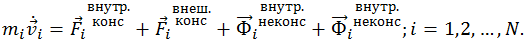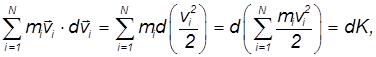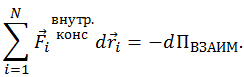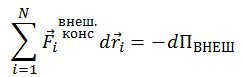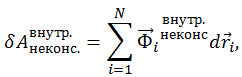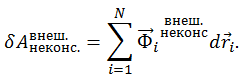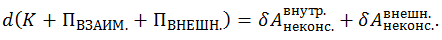4.5. Закон сохранения энергии

Рассмотрим систему из N материальных точек с массами m₁, m₂, ..., m_N. Предположим, что на точку с номером i действуют: 1) суммарная внутренняя консервативная сила , 2) суммарная внутренняя неконсервативные сила , 3) суммарная внешняя консервативная сила и 4) суммарная внешняя неконсервативная сила . Тогда уравнение движения i-ой точки имеет вид (4.5.1)

(4.5.1)

Умножим обе части уравнения (4.5.1) на элементарное перемещение

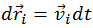
и сложим все уравнения для точек с номерами i = 1, ..., N. При этом учтем, что

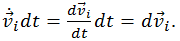
Получим

(4.5.2)

Рассмотрим по отдельности каждый член в этом уравнении. В левой части стоит величина

(4.5.3)

которая с очевидностью является приращением полной кинетической энергии К частиц системы.

Первое слагаемое в правой части (4.5.2) есть суммарная работа всех внутренних консервативных сил. Второе слагаемое есть суммарная работа всех внешних консервативных сил. В силу консервативности сил и то и другое слагаемые можно представить в виде убыли соответствующей потенциальной энергии. В первом случае — внутренние — консервативные силы, в виде убыли потенциальной энергии взаимодействия тел системы:

(4.5.4)

Во втором случае — внешние — консервативные силы, в виде убыли потенциальной энергии системы во внешнем консервативном силовом поле

(4.5.5)

Третье и четвертое слагаемые представляют суммарную работу внутренних и внешних неконсервативных сил и потому не могут быть представлены в виде убыли некоторой скалярной функции только координат по той простой причине, что таковая не существует. Введем для этих слагаемых следующие обозначения: элементарная работа всех внутренних неконсервативных сил

(4.5.6)

и элементарная работа всех внешних неконсервативных сил

(4.5.7)

Перенесем (4.5.4) и (4.5.5) налево и используем обозначения (4.5.6) и (4.5.7), тогда уравнение (4.5.2) приобретет вид.

(4.5.8)

Стоящая в левой части под знаком дифференциала сумма, по определению есть полная механическая энергия системы.

(4.5.9)

Таким образом, окончательно мы получаем соотношение, которое можно назвать теоремой о приращении полной механической энергии:

(4.5.10)

которая гласит: приращение механической энергии системы равно суммарной работе всех неконсервативных сил, как внутренних, так и внешних.

Как следует из (4.5.10), если система замкнута, то приращение её механической энергии равно работе внутренних неконсервативных сил. То есть одного только факта замкнутости системы (отсутствия внешних сил) недостаточно для того, чтобы механическая энергия сохранялась. Достаточным является полное отсутствие — как среди внешних, так и среди внутренних — неконсервативных сил.

Таким образом, закон сохранения механической энергии гласит:

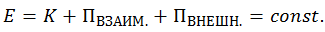
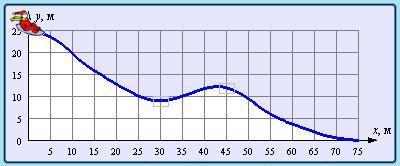
Рис.4.11. Ускорение материальной точки равно нулю в точках экстремумов потенциальной энергии.

Отсюда и название: консервативные (to conserve — беречь, охранять, сберегать, сохранять) силы это такие силы, при действии которых механическая энергия сохраняется/

Закон сохранения механической энергии замкнутой системы можно сформулировать так:

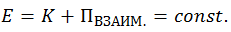
Налицо явное отличие закона сохранения механической энергии замкнутой системы от закона сохранения импульса замкнутой системы: импульс замкнутой системы сохраняется вне зависимости от характера сил, действующих внутри системы, а механическая энергия замкнутой системы сохраняется только тогда, когда внутри замкнутой системы отсутствуют неконсервативные силы. Это легко понять. Механический импульс системы

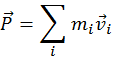
это весь импульс, какой только может быть — другого импульса не существует. А механическая энергия системы (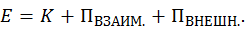) это не вся её энергия — не учтена внутренняя (тепловая, химическая и т. п.) энергия тел, входящих в состав системы. Неконсервативные силы тем и занимаются, что переводят механическую энергию во внутреннюю, или наоборот, внутреннюю энергию в механическую. Подчеркнем, что механическая энергия замкнутой системы, в результате действия внутри неё неконсервативных сил, может не только убывать, но и возрастать. Например, при взрыве летящего снаряда, суммарная кинетическая энергия его осколков и образовавшихся при взрыве пороховых газов больше, чем кинетическая энергия снаряда (вместе с порохом внутри) непосредственно перед взрывом. Для того, чтобы это было вполне очевидным, перейдем в ту систему отсчета, в которой снаряд непосредственно перед взрывом покоится (в систему его центра масс). Все части снаряда неподвижны, значит полная кинетическая энергия равна нулю. После взрыва осколки снаряда и пороховые газы движутся — кинетическая энергия больше нуля и равна энергии, выделившейся при сгорании пороха.

Видео 4.3. Тепловой взрыв. Работа силы трения увеличивает внутреннюю энергию газа, в определенный момент она высвобождается, превращаясь в кинетическую энергию «снаряда».

Закон сохранения энергии является всеобъемлющим постольку, поскольку всеобщим является постулат об однородности времени для замкнутой системы, а общее определение энергии таково: энергия это сохраняющаяся характеристика замкнутой системы, сохранение которой обусловлено однородностью времени. Пока мы — в этом учебнике — имеем дело только с механической энергией, но есть и другие ее формы, в том числе, без сомнения, нам (человечеству) пока неизвестные. Например, совсем недавно астрофизики обнаружили наличие некоторого вида материи, которую назвали «темной материей». На сегодняшний день (начало 2010 года) про неё известно только то, что она подвержена гравитационному притяжению. Если обнаруживается, что в каком-либо физическом процессе энергия не сохраняется, мы ищем новую форму энергии, чтобы обеспечить ее точный баланс. Поступая так, мы вовсе не «жульничаем» и не делаем нечестной попытки скрыть недостаток наших знаний о природе. Так ученые «придумали» тепловую, электромагнитную, ядерную и др. формы энергии. Один из основоположников теории относительности Анри Пуанкаре писал: «Поскольку мы не в состоянии дать общее определение энергии, закон сохранения энергии следует рассматривать просто, как указание на то, что существует «нечто», остающееся постоянным (в любом физическом процессе). К каким бы открытиям ни привели нас будущие эксперименты, мы заранее знаем, что и тогда будет «нечто», обладающее способностью сохраняться, и это нечто мы, скорее всего, сможем называть энергией».

Видео 4.4. Цепочка переходов энергии из одного вида в другой: химической в механическую, механической в электромагнитную.

Сохранение энергии и переход ее из одной формы в другую демонстрируется в опыте с маятником Максвелла (Видео 4.5.).

Видео 4.5. Маятник Максвелла. При рассмотрении баланса энергий необходимо учитывать кинетическую энергию не только поступательного, но и вращательного движения.

Дополнительная информация

http://www.plib.ru/library/book/17005.html — Стрелков С.П. Механика Изд. Наука 1971 г. – стр. 210–211 (§58): маятник Максвелла.