4.6. Условия равновесия механической системы

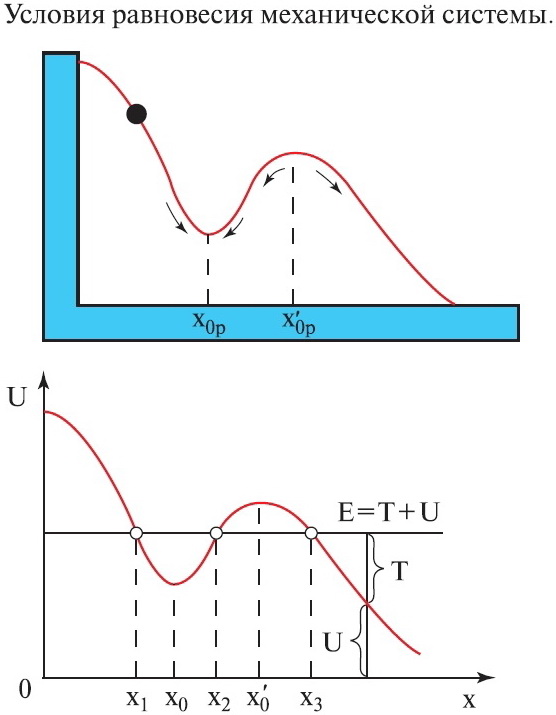
Закон сохранения энергии позволяет провести анализ общих закономерностей движения, если известна зависимость потенциальной энергии от координат. Рассмотрим для примера одномерное движение материальной точки (частицы), вдоль оси 0x в потенциальном поле, показанном на рис. 4.12.

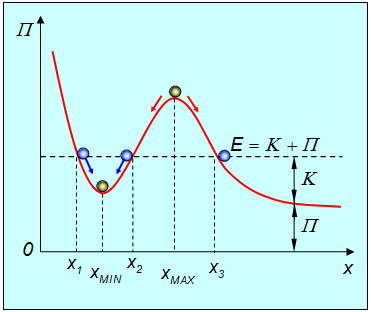
Рис.4.12. Движение частицы вблизи положений устойчивого и неустойчивого равновесия

Поскольку в однородном поле сил тяжести потенциальная энергия пропорциональна высоте подъема тела, можно представить себе ледяную горку (пренебрегаем трением) с профилем, соответствующим функции П(x) на рисунке.

Из закона сохранения энергии E = К + П и из факта, что кинетическая энергия К = Е - П всегда неотрицательна, следует, что частица может находиться лишь в областях, где E > П. На рисунке частица с полной энергией E может двигаться только в областях

В первой области ее движение будет ограничено (финитно): при данном запасе полной энергии частица не может преодолеть «горок» на своем пути (их называют потенциальными барьерами) и обречена вечно оставаться в «долине» между ними. Вечно — с точки зрения классической механики, которую мы сейчас изучаем. В конце курса мы увидим, как квантовая механика помогает частице выбраться из заточения в потенциальной яме — области

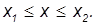
Во второй области движение частицы не ограничено (инфинитно), она может удалиться бесконечно далеко от начала координат направо, но слева ее движение по-прежнему ограничено потенциальным барьером:

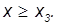
Видео 4.6. Демонстрация финитного и инфинитного движений.

В точках экстремума потенциальной энергии x_MIN и x_MAX сила, действующая на частицу, равна нулю, потому что равна нулю производная потенциальной энергии:

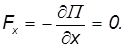
Если поместить в эти точки покоящуюся частицу, то она оставалась бы там ... опять-таки вечно, если бы не флуктуации ее положения. В этом мире нет ничего строго покоящегося, частица может испытывать небольшие отклонения (флуктуации) от положения равновесия. При этом, естественно, возникают силы. Если они возвращают частицу к положению равновесия, то такое равновесие называется устойчивым. Если же при отклонении частицы возникающие силы еще дальше уводят ее от равновесного положения, то мы имеем дело с неустойчивым равновесием, и частица в таком положении обычно долго не задерживается. По аналогии с ледяной горкой можно догадаться, что устойчивым будет положение в минимуме потенциальной энергии, а неустойчивым — в максимуме.

Докажем, что это действительно так. Для частицы в точке экстремума x_M (x_MIN или x_MAX) действующая на нее сила F_x(x_M) = 0. Пусть вследствие флуктуации координата частицы изменяется на небольшую величину 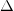x. При таком изменении координаты на частицу начнет действовать сила

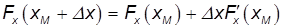
(штрихом обозначена производная по координате x). Учитывая, что F_x=-П', получаем для силы выражение

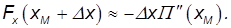
В точке минимума вторая производная потенциальной энергии положительна: U"(x_MIN) > 0. Тогда при положительных отклонениях от положения равновесия 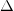x > 0 возникающая сила отрицательна, а при 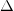x<0 сила положительна. В обоих случаях сила препятствует изменению координаты частицы, и положение равновесия в минимуме потенциальной энергии устойчиво.

Наоборот, в точке максимума вторая производная отрицательна: U"(x_MAX)<0. Тогда увеличение координаты частицы Δx приводит к возникновению положительной же силы, еще больше увеличивающей отклонение от положения равновесия. При 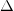x<0 сила отрицательна, то есть и в этом случае способствует дальнейшему отклонению частицы. Такое положение равновесия неустойчиво.

Таким образом, положение устойчивого равновесия может быть найдено при совместном решении уравнения и неравенства

Видео 4.7. Потенциальные ямы, потенциальные барьеры и равновесие: устойчивое и неустойчивое.

Пример. Потенциальная энергия двухатомной молекулы (например, Н₂ или О₂) описывается выражением вида

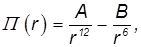
где r — расстояние между атомами, а A, B — положительные постоянные. Определить равновесное расстояние r_М между атомами молекулы. Устойчива ли двухатомная молекула?

Решение. Первый член описывает отталкивание атомов на малых расстояниях (молекула сопротивляется сжатию), второй — притяжение на больших расстояниях (молекула сопротивляется разрыву). В соответствии со сказанным, равновесное расстояние находится при решении уравнения

Дифференцируя потенциальную энергию, получаем

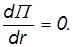
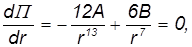
откуда

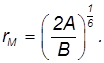
Находим теперь вторую производную потенциальной энергии

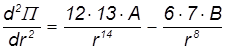
и подставляем туда значение равновесного расстояния r_M :

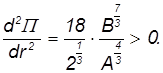
Положение равновесия устойчиво.

На рис. 4.13 представлен опыт по изучению потенциальных кривых и условий равновесия шарика. Если на модели потенциальной кривой поместить шарик на высоту большую высоты потенциального барьера (энергия шарика больше энергии барьера), то шарик преодолевает потенциальный барьер. Если начальная высота шарика меньше высоты барьера, то шарик остается в пределах потенциальной ямы.

Шарик, помещенный в наивысшую точку потенциального барьера, находится в неустойчивом равновесии, поскольку любое внешнее воздействие приводит к переходу шарика в нижнюю точку потенциальной ямы. В нижней точке потенциальной ямы шарик находится в устойчивом равновесии, поскольку любое внешнее воздействие приводит к возвращению шарика в нижнюю точку потенциальной ямы.

Рис. 4.13. Экспериментальное изучение потенциальных кривых

Дополнительная информация

http://vivovoco.rsl.ru/quantum/2001.01/KALEID.PDF – Приложение к журналу «Квант» — рассуждения об устойчивом и неустойчивом равновесии (А. Леонович);

http://mehanika.3dn.ru/load/24-1-0-3278 – Тарг С.М. Краткий курс теоретической механики, Изд,Высшая школа, 1986 г. – стр. 11–15, §2 – исходные положения статики.