4.7. Примеры применения законов сохранения

Приведем вначале примеры задач-оценок, когда не требуется точного решения, но лишь более или менее адекватная оценка порядков величин.

Пример 1. Гвоздь забили пятью ударами молотка. Оценить, какую силу надо приложить, чтобы выдернуть гвоздь.

Решение. Пусть m — масса молотка, a — его скорость в момент удара. Для оценки можно предположить, что гвоздю передается вся кинетическая энергия молотка. При n ударах эта энергия равна

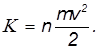
Энергия гвоздя расходуется на преодоление силы трения F при вхождении гвоздя в стену: при углублении гвоздя на расстояние l совершается работа

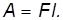
Из равенства A = К находим

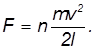
Эта же сила препятствует вытаскиванию гвоздя. Для численной оценки примем разумные исходные данные: m = 1 кг, v = 5 м/с, l = 5 см. Получаем тогда:

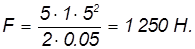
Эта сила примерно эквивалентна весу массы в 130 кг.

При решении мы пренебрегли потерями энергии на нагревание молотка, гвоздя и стенки, но перед нами стояла задача получить всего лишь оценку, а не точное решение.

Пример 2. Оценить мощность выделения тепла при экстренном торможении грузовика.

Решение. Пусть m — масса грузовика, который двигался со скоростью . Кинетическая энергия грузовика до торможения равна

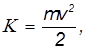
после — нулю. Разность этих кинетических энергий перешла в тепло:

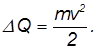
Среднюю скорость грузовика в процессе торможения можно принять равной /2. Если тормозной путь равен l , то до остановки грузовика прошло время

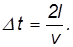
Отсюда находим мощность выделения тепла:

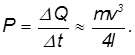
Для численной оценки примем: m = 10 т, v = 72 км/час, l = 20 м. Тогда находим:

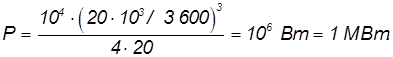
Дополнительная информация

http://www.plib.ru/library/book/17005.html – Стрелков С.П. Механика Изд. Наука 1971 г. – стр.134–135 (§37): маятник Галилея (закон сохранения энергии);

Приведем теперь примеры совместного использования законов сохранения импульса и энергии при изучении соударения двух тел. При столкновении тела претерпевают деформацию. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Увеличение внутренней энергии тел приводит к повышению их температуры. Существует два предельных типа удара: абсолютно упругий и абсолютно неупругий.

При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга, и разлетаются со скоростями, величина и направление которых определяются двумя условиями — сохранением полной энергии и сохранением полного импульса системы двух тел.

Видео 4.9. Упругое столкновение тележек. «Обмен скоростями» при равенстве масс упруго сталкивающихся тел.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии упругой деформации не возникает: кинетическая энергия тел полностью или частично превращается во внутреннюю (тепловую) энергию.

При абсолютно неупругом ударе тел работает лишь закон сохранения импульса, механическая энергия не сохраняется, переходит в тепловую (внутреннюю), поэтому имеет место закон сохранения суммарной энергии — механической и внутренней.

Пусть два сталкивающихся шара образуют замкнутую систему. Рассмотрим сначала абсолютно неупругий удар (рис. 4.16).

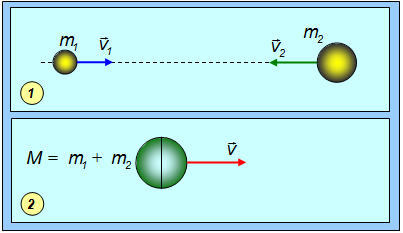
Рис. 4.16. Абсолютно неупругое столкновение двух шаров: 1 — состояние до удара; 2 — состояние после удара

Начальные скорости шаров ₁ и ₂, а их массы m₁ и m₂ конечная скорость шаров — . При соударении выполняется закон сохранения импульса:

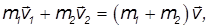
откуда находим скорость образовавшейся составной частицы

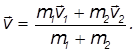
Как и следовало ожидать, соединившиеся шары после соударения продолжают двигаться со скоростью центра масс системы до соударения.

Энергия, перешедшая при этом во внутреннюю энергию шаров, равна разности кинетических энергий до и после соударения:

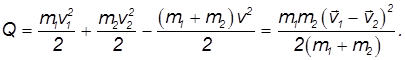
где 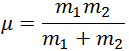— так называемая, «приведенная масса» шаров, а 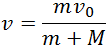— относительная скорость шаров до удара, а именно: скорость до удара второго шара ( 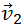минус 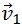) относительно первого. Отсюда видно, что Q равно кинетической энергии относительного движения шаров до удара. Только эта часть полной кинетической энергии шаров до удара может полностью перейти в тепловую (внутреннюю) энергию. Поэтому абсолютно неупругий удар можно определить и так: при абсолютно неупругом ударе вся энергия относительного движения переходит в тепловую (внутреннюю) энергию.

Видео 4.10. Абсолютно неупругое столкновение шаров в системе центра масс и в лабораторной системе отсчета.

Пример 3. Артиллеристы стреляют так, чтобы ядро попало в неприятельский лагерь, находящийся на расстоянии l₀ = 7.2 км от пушки. В момент вылета ядра из дула на него вскакивает барон Мюнхаузен (абсолютно неупругий удар), масса которого в n = 5 раз больше массы ядра. Из-за этого ядро падает, не долетев до цели. Какое расстояние барону придется пройти пешком, чтобы добраться до неприятельского лагеря? Сопротивлением воздуха пренебречь.

Решение. Если ядро вылетело из дула со скоростью ₀, то после вскакивания на него барона его скорость стала равной

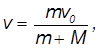
где m — масса ядра, а М — масса Мюнхгаузена. Пользуясь формулами темы 2.7, артиллеристы рассчитывали угол возвышения 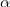орудия по формуле

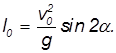
Поскольку скорость изменилась, а угол остался прежним, дальность полета составит

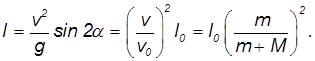
Поэтому барону надо будет пройти расстояние

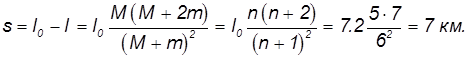
Иными словами, барону удалось пролететь на ядре только 200 м.

Дополнительная информация

http://www.plib.ru/library/book/14978.html – Сивухин Д.В. Общий курс физики, том1, Механика Изд. Наука 1979 г. – стр.157 (§28, задачи 14, 15): обсуждаются ядерные реакции управляемого термоядерного синтеза.

Теперь рассмотрим абсолютно упругий удар. Ограничимся случаем центрального удара двух однородных шаров. Удар называется центральным, если векторы скорости центров шаров до удара направлены вдоль прямой, проходящей через центры сталкивающихся шаров (рис. 4.17).

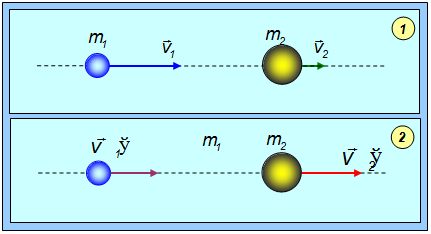
Рис. 4.17. Абсолютно упругое центральное соударение двух шаров: 1 – состояние до удара; 2 – состояние после удара

Шары рассматриваем как материальные точки, то есть пренебрегаем их возможным вращением. Как и в предыдущем случае, пренебрежем также трением о поверхность, по которой движутся шары. Напишем уравнения сохранения механической энергии и импульса.

В рассматриваемом случае центрального удара скорости шаров после удара будут направлены вдоль той же прямой, по которой двигались центры шаров перед ударом. Поэтому векторы скоростей можно заменить их проекциями на линию соударения:

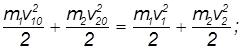
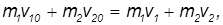
где m₁ и m₂ — массы шаров, v₁₀ и v₂₀ — скорости шаров до удара и v₁ и v₂ — скорости шаров после удара (скорости понимаются в алгебраическом смысле: знак указывает направление движения вдоль линии соударения).

Преобразуем уравнения сохранения энергии и импульса к виду:

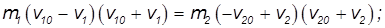
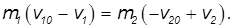
Выражения, стоящие в левой и правой частях уравнений, будем считать отличными от нуля (иначе v₁₀ = v₁ и v₂₀ = v₂ — скорости шаров не изменились, то есть столкновения не произошло). Разделим первое уравнение на второе, после чего получим:

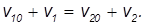
Умножим полученное уравнение на m₂ и вычтем из него преобразованное уравнение закона сохранения импульса. Находим:

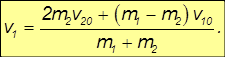
Аналогично умножим полученное уравнение на m₁ и сложим с ним преобразованное уравнение закона сохранения импульса. Получим:

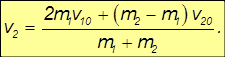
В отличие от неупругого столкновения, здесь скорости шаров после соударения не могут быть равны. В самом деле, если v₁ = v₂, то из полученных выражений для скоростей шаров после удара следует, что до соударения скорости тоже были равны v₁₀ = v₂₀. Но в этом случае соударение не может произойти. При центральном ударе шары столкнутся, если они движутся навстречу друг другу или один шар догоняет другой.

Анализ полученных соотношений

1. Если второй шар первоначально покоился (v₂₀ = 0), то после соударения скорости шаров определяются соотношениями

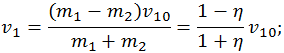
Здесь η = m₂/m₁ — отношение масс сталкивающихся шаров. Отметим, что при заданной скорости налетающего шара до столкновения, скорости шаров после столкновения определяются исключительно отношением масс шаров.

Знак скорости v₂ совпадает со знаком v₁₀: покоившийся шар обязательно начнет двигаться в направлении движения налетающего шара. Знак скорости v₁ зависит от соотношения масс шаров: если покоившийся шар более массивен, то налетавший отскочит в обратном направлении, если более массивен налетающий шар, он продолжит движение в том же направлении. При равенстве масс налетающий шар остановится.

Рассмотрим два предельных случая:

• Масса покоящегося шара гораздо больше массы налетающего: m₂ >> m₁ или η>>1.

  Тогда

  

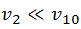
  (то есть тяжелый шар остается неподвижным) и

  

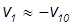
  (легкий шар отскакивает с той же скоростью в обратном направлении).

• Масса налетающего шара намного превосходит массу покоящегося: m₁>>m₂ или η<<1.

  Тогда

  

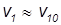
  (тяжелый шар не меняет своей скорости) и

  

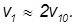
2. Если массы шаров равны (m₁ = m₂ или η=1), то из полученных формул для скоростей шаров после столкновения следует

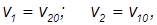
то есть шары при соударении обмениваются скоростями. С частным случаем этого явления мы познакомились выше: до соударения покоился шар 2, после — шар 1.

3. Если оба шара двигаются, но масса одного шара много больше массы другого (m₂>>m₁), то

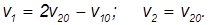
Иначе говоря, массивный шар не "замечает" соударения с легким шаром и продолжает двигаться с прежней скоростью. Скорость же легкого шара меняется. Мы получили комбинацию полученных ранее результатов.

Законы столкновения шаров иллюстрируются с помощью интерактивной компьютерной модели (рис. 4.18).

Рис. 4.18. Исследование законов столкновения шаров с помощью интерактивной компьютерной модели

Пусть имеется ряд одинаковых соприкасающихся упругих шаров. С крайним шаром ряда сталкивается такой же шар, движущийся со скоростью v₀ (рис. 4.19). В результате удара он останавливается, а последний шар ряда начинает двигаться с той же скоростью v₀.

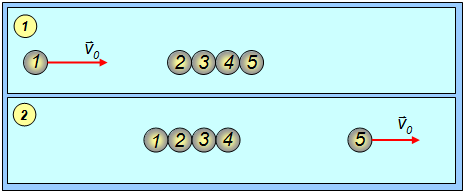
Рис 4.19. Упругое столкновение шара с несколькими покоящимися шарами: 1 – положение до соударения; 2 – после соударения

Это явление объясняется тем, что при столкновении шаров 1 и 2 шар 1 останавливается, а шар 2 приобретает скорость v₀. Шар 2 тут же сталкивается с шаром 3 и останавливается и т. д.

Пусть на неподвижный ряд одинаковых шаров налетают два таких же шара, движущихся со скоростью v₀ каждый (рис. 4.20).

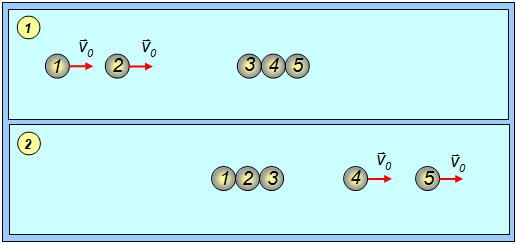
Рис 4.20. Упругое столкновение двух шаров с несколькими покоящимися шарами: 1 – положение до соударения; 2 – после соударения.

Сначала при столкновении шара 2 с шаром 3, шар 2 останавливается, а шар 3 приобретает скорость v₀, передавая её шару 4 и т. д. Сразу же после этого шар 1 сталкивается с шаром 2, останавливается, передавая свою скорость шару 2, и процесс повторяется. В результате все шары, кроме двух последних, движущихся со скоростями v₀, остаются неподвижными.

Центральные упругие столкновения в цепочке одинаковых шаров демонстрируются на рис. 4.21.

Рис. 4.21. Центральные столкновения в цепочке одинаковых шаров

Здесь все шары подвешены на длинных нитях, и задача сводится к изучению их попарных столкновений. При этом крайние шары будут поочередно отскакивать с одинаковой скоростью и отклоняться на нитях на одинаковые углы, а все остальные шары, находящиеся между ними, будут находиться в состоянии покоя.

Видео 4.11. Нецентральное упругое столкновение шаров одинаковой массы. Эффект вращения шаров после удара.

Знакомство с конкретными примерами позволяет сформулировать общие важные положения. Не все из них вытекают, правда, из вышесказанного, но это и не удивительно: само понятие энергии гораздо шире его проявления в механике, и мы только начинаем с ним знакомиться. Итак:

• Законы сохранения носят фундаментальный характер и тесно связаны с симметрией пространства и времени. Закон сохранения энергии связан с однородностью времени, то есть равнозначностью всех моментов времени. Закон сохранения импульса связан с однородностью пространства, то есть равнозначностью всех точек пространства.
• Законы сохранения носят общий характер и не зависят от конкретной системы и ее движения. Из законов сохранения вытекает, что какие-то процессы заведомо оказываются невозможными. Так, в 1775 г. Французская Академия решила не принимать к рассмотрению проекты вечных двигателей как противоречащих закону сохранения энергии.
• Законы сохранения позволяют рассмотреть общие свойства движения без решения уравнений и детальной информации о протекании процессов во времени. Поэтому законы сохранения могут быть использованы даже в тех случаях, когда силы точно не известны. Так, в частности, обстоит дело в физике элементарных частиц. Даже в тех случаях, когда силы заданы в точности, законы сохранения могут оказать существенную помощь при решении задач о движении частиц.

Дополнительная информация

http://www.plib.ru/library/book/17005.html – Стрелков С.П. Механика Изд. Наука 1971 г. – стр.122–126 (§34): упругий нецентральный удар шаров;

http://www.plib.ru/library/book/14978.html – Сивухин Д.В. Общий курс физики, том1, Механика Изд. Наука 1979 г. – стр. 151–154 (§28, п.п.4–6): абсолютно упругое соударение шаров рассматривается в системе центра масс;

http://kvant.mirror1.mccme.ru/1993/05/povest_o_tom_kak_stolknulis_dv.htm – Журнал «Квант» – о столкновении двух упругих шаров (А. Гросберг).