4.8. Закон сохранения момента импульса

Мы уже говорили, что законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмерного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство изотропно, в нем нет выделенных направлений. С этой симметрией связан закон сохранения момента импульса. Эта связь проявится в том, что момент количества движения, как мы увидим в дальнейшем, является одной из основных величин, описывающих вращательное движение.

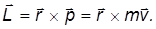
Направление вектора L определяется по правилу буравчика (штопора), а его величина равна

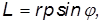
где 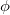— угол между векторами r и р. Величина l = r 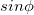равна расстоянию от начала координат 0 до прямой, вдоль которой направлен импульс частицы. Эта величина называется плечом импульса (рис. 4.22). Вектор L зависит от выбора начала координат, поэтому говоря о нем, обычно указывают: «момент импульса относительно точки 0».

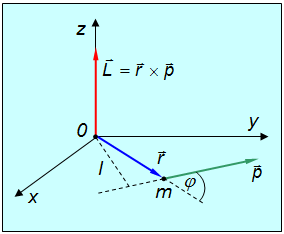
Рис. 4.22. Момент импульса L частицы массой m

Рассмотрим производную по времени от момента импульса:

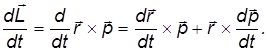
Первое слагаемое равно нулю, так как 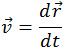и 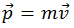очевидным образом параллельны

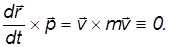
Во втором слагаемом, согласно второму закону Ньютона, производную импульса можно заменить на силу, действующую на частицу.

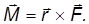
Направление момента силы определяется тем же правилом буравчика. Его величина

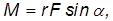
где 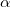— угол между радиус-вектором и силой. Аналогично тому, как это было сделано выше, определяется и плечо силы l = r 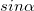— расстояние от точки 0 до линии действия силы. В итоге из полученного в результате дифференцирования соотношения находим уравнение движения для момента импульса частицы:

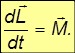
По форме уравнение аналогично второму закону Ньютона: вместо импульса частицы стоит момент импульса, а вместо силы — момент силы.

Если M = 0, то L = const, то есть

Для центральных сил

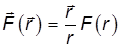
и момент силы относительно силового центра равен нулю:

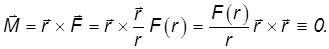
Таким образом, для центральных сил

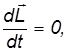
то есть L = const.

Другими словами,

Отсюда вытекает важное следствие. Поскольку момент импульса ортогонален плоскости, задаваемой импульсом тела и радиус-вектором, проведенным из центра сил, эта плоскость не меняет своего положения со временем. Иными словами, орбита каждого тела в поле центральных сил лежит в одной плоскости, проходящей через центр сил (хотя для разных тел эти плоскости могут различаться). Таким образом, в поле центральных сил невозможны, например, винтовые траектории.

Рассмотрим теперь систему, состоящую из двух взаимодействующих частиц (рис. 4.23).

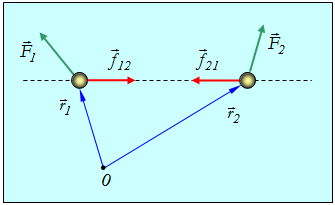
Рис. 4.23. Система, состоящая из двух взаимодействующих частиц

Уравнения движения этих частиц имеют вид:

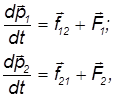
где F₁ и F₂ — внешние силы, a f₁₂=-f₂₁ — внутренние силы взаимодействия между частицами, направленные вдоль линии, их соединяющей

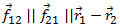
Умножим первое уравнение векторно слева на радиус-вектор первой частицы r₁, а второе — векторно слева на радиус-вектор второй частицы r₂

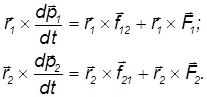
Учтем, что

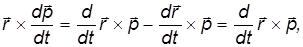
поскольку

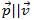
и

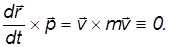
Используя третий закон Ньютона f₁₂ = –f₂₁, перепишем систему уравнений движения частиц в виде:

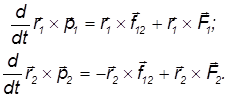
Сложим полученные соотношения:

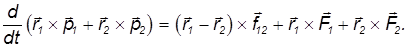
Имеет место соотношение между векторами

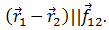
Поэтому их векторное произведение равно нулю.

Таким образом, мы получаем

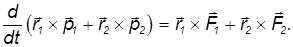
В левой части равенства стоит производная от суммы моментов импульса частиц (ее называют полным моментом импульса L системы), а в правой — сумма моментов внешних сил — полный момент М внешних сил, действующих на тела системы. Обобщение на случай системы из многих частиц (или твердого тела) очевидно.

Момент импульса системы N частиц равен

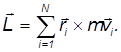
Полный момент внешних сил будет

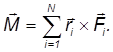
Уравнение, определяющее изменение во времени момента импульса системы частиц имеет вид:

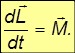
Отсюда следует, что при М = 0 и, соответственно, L = const следует закон сохранения момента импульса системы:

Видео 4.12. Демонстрация закона сохранений момента импульса: стрельба из пушки, установленной на вращающейся платформе по касательной, по диаметру и «кривым» снарядом.

Пример. Выясним, при каких условиях момент импульса системы не зависит от выбора начала координат 0.

Найдем сначала, как изменяется момент импульса при смене начала координат. Возьмем некую точку 0', положение которой относительно точки 0 задается радиус-вектором r₀. Радиус-векторы r_i', проведенные из 0', связаны с радиус-векторами r_i соотношениями

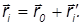
Подставим это выражение в формулу для момента импульса L относительно точки 0 :

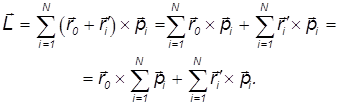
В первом члене мы введем полный импульс системы

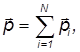
а второй член есть не что иное, как момент импульса L' относительно точки 0'.

Имеем

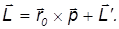
Мы ищем условие, когда

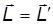
для произвольного вектора r₀. Это возможно только при равенстве нулю полного импульса системы р = 0. Иными словами, момент импульса не зависит от выбора начала координат в системе отсчета, связанной с центром масс системы.