4.9. Движение частицы в центральном силовом поле
Рассмотрим более подробно движение частицы в центральном силовом поле. Как уже отмечалось выше, ее момент импульса относительно силового центра сохраняется
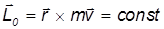
или в скалярной форме

Пусть перемещение частицы за время dt есть vdt. Площадь, «заметаемая» радиус-вектором частицы (заштрихована на рис. 4.24) за это время, будет
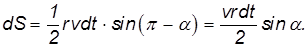
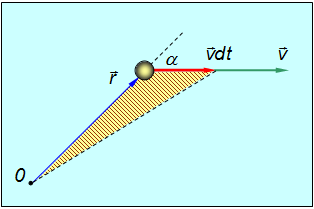
Рис. 4.24. Cекториальная скорость частицы
Площадь, заметаемая радиус-вектором частицы в единицу времени, называется секториальной скоростью:
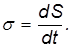
Подставляя выражение для площади в формулу для секториальной скорости, получим
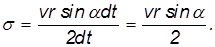
Учитывая, что
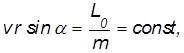
приходим к закону площадей.
Секториальная скорость частицы, движущейся в центральном силовом поле, является постоянной величиной:
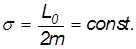
Пример. Пусть спутник движется вокруг Земли по эллиптической орбите (рис. 4.25), причем минимальное и максимальное удаление от Земли составляет Rmin и Rmax. Найдем его скорость в перигее и апогее.
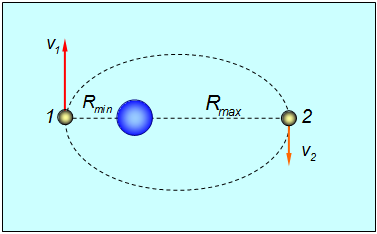
Рис. 4.25. Движение спутника по эллиптической орбите вокруг Земли
Запишем в точках 1 и 2 закон сохранения момента импульса для спутника:
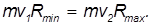
Запишем для тех же точек закон сохранения энергии:
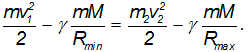
Выражая v2 из закона сохранения момента импульса
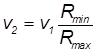
и подставляя полученное выражение в закон сохранения энергии, находим искомые скорости
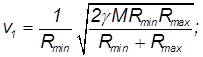
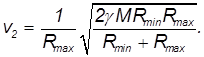
Видно, что в точке минимального удаления скорость спутника максимальна, и, наоборот, в точке максимального удаления его скорость минимальна.


