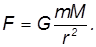5.1. Законы Кеплера

Возможно, падающее яблоко и наводит на определенные мысли, но за 50 лет до Ньютона уже были известны количественные соотношения, которые прокладывали более прямой путь к установлению закона всемирного тяготения. Одним из величайших открытий в астрономии стали установленные И. Кеплером (1571–1630) законы движения планет:

Рис. 5.1. Орбита планеты, движущейся по эллиптической орбите вокруг Солнца

Коль скоро планеты обращаются вокруг Солнца благодаря силе, с которой светило действует на них, то законы Кеплера позволяют определить вид этой силы. Поместим начало координат в центр Солнца. Пусть — радиус-вектор планеты, a 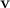— ее скорость в данный момент времени. За время перемещение планеты равно 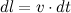и направлено под углом а к радиус-вектору. Площадь 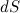треугольника, образованного векторам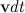и , и +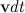, равна — (рис. 5.2).

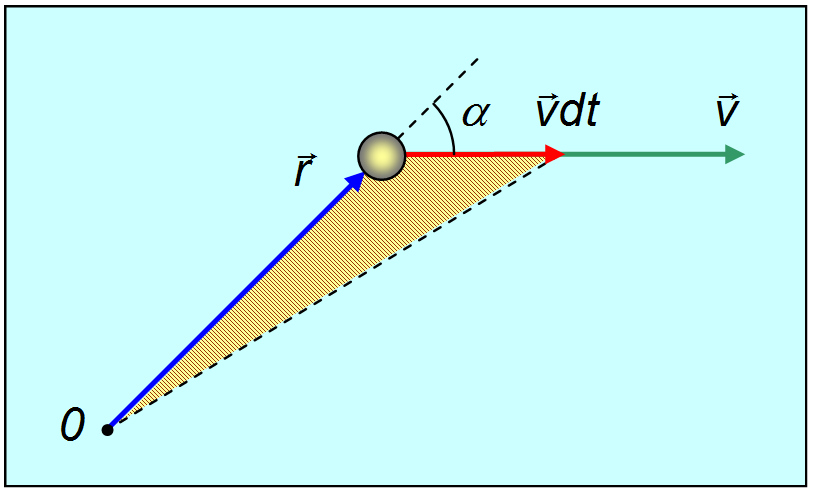
Рис. 5.2. Секториальная скорость

Согласно второму закону Кеплера, величина

остается постоянной. Первый закон Кеплера утверждает, в частности, что орбита планеты лежит в одной плоскости. Это значит, что не зависит от времени вектор

величина которого равна 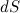/, а направление ортогонально плоскости орбиты. Этот вектор, называемый секториальной скоростью, пропорционален моменту импульса планеты

Отсюда следует, что силы, действующие на планету, — центральные: они направлены по линии, соединяющей Солнце с планетой, и зависят лишь от расстояния до Солнца.

Третий закон Кеплера позволяет установить зависимость сил от расстояния. Частный случай эллиптической орбиты - это круговая орбита, в центре которой находится Солнце. Тогда второй закон Кеплера сводится к утверждению о постоянстве угловой скорости 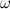обращения планеты. Напомним, что угловая скорость обратно пропорциональна периоду обращения T:

Для этого случая третий закон Кеплера утверждает, что отношение квадратов периодов обращения планет равен отношению кубов радиусов их орбит, то есть что квадраты периодов пропорциональны кубам радиусов орбит:

Отсюда следует, что квадраты угловых скоростей обратно пропорциональны кубам радиусов:

Комбинация 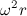есть не что иное как нормальное ускорение, которое для равномерного вращения по окружности совпадает с полным ускорением 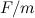, где 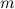— масса планеты. Таким образом, получаем, что

Таким образом, Солнце притягивает планету с силой, пропорциональной массе планеты и обратно пропорциональной квадрату расстояния до него:

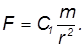
Здесь 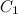— коэффициент пропорциональности. Соответственно, планета притягивает Солнце с такой же силой, которая может быть выражена как

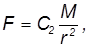
где 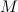— масса Солнца, а 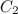— какой-то другой коэффициент пропорциональности. Из равенства модулей (третий закон Ньютона) вытекает соотношение

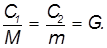
Обозначенное символом 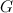отношение коэффициентов пропорциональности к массе называется гравитационной постоянной. Подставляя значения

в выражения для силы гравитации между Солнцем и планетой, находим