5.2. Гравитационные силы

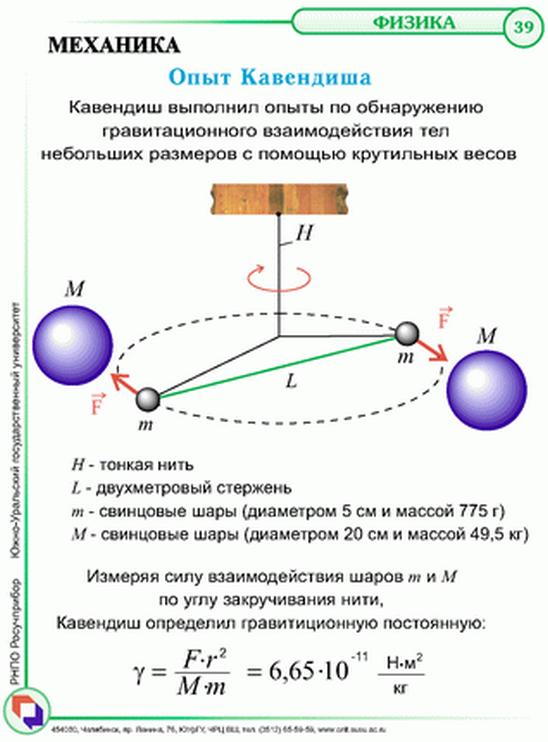
Рис. 5.3. Опыт Кавендиша по измерению силы гравитационного притяжения

Обобщая полученное соотношение, можно утверждать, что силы гравитации между любыми двумя телами определяются массами взаимодействующих тел и расстояниями между ними. Согласно установленному закону всемирного тяготения,

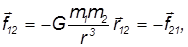
где гравитационная постоянная 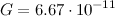м³/(кг·с²), а 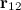— радиус-вектор второго тела относительно первого (рис. 5.4). Знаки минус указывают на то, что силы взаимодействия являются силами притяжения и противоположно направлены.

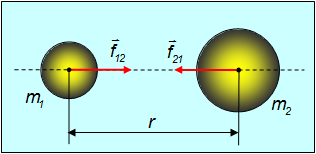
Рис. 5.4. Силы гравитации между двумя телами

Наиболее точно гравитационная постоянная определяется по изменению периода колебаний крутильных весов, вызванному приближением притягивающихся масс. Первые измерения относятся к концу XVIII столетия, из них классическим является опыт Г. Кавендиша (1798 г.).

Схема опыта Кавендиша заключается в использование крутильных весов (рис. 5.5).

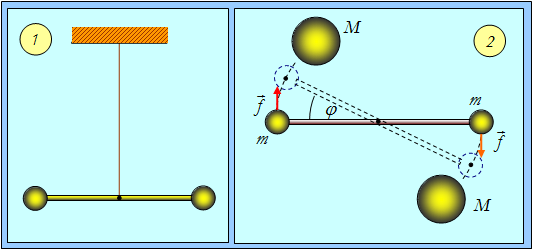
Рис.5.5. Опыт Кавендиша: 1 — крутильные весы; 2 — вид сверху

На тонкой кварцевой нити подвешено коромысло с двумя небольшими свинцовыми шариками. При приближении к ним массивных свинцовых шаров нить закручивается. Измеряя угол поворота коромысла 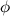и зная модуль кручения нити, можно непосредственно измерить силу взаимодействия. Зная массы шаров и расстояние между ними, из закона всемирного тяготения можно определить гравитационную постоянную:

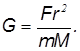
Функционирование установки, которую использовал Кавендиш, показано на рис. 5.3.

Если тела нельзя считать материальными точками, их представляют как совокупность материальных точек (частиц) и, геометрически суммируя силы взаимодействия отдельных частиц, находят результирующую силу тяготения между ними. Можно показать, что для тел идеально сферической формы закон гравитационного взаимодействия будет таким же, как и для материальных точек, если считать, что радиус-вектор 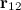соединяет центры сфер (см. рис. 5.4).