5.3. Характерные астрономические масштабы
Закон всемирного тяготения позволяет установить масштабы расстояний и масс в Солнечной системе.
Радиус Земли можно найти с помощью геометрических измерений на ее поверхности. Первым это сделал Эратосфен (276–194 г. до н.э.), нашедший для радиуса Земли величину R3 = 6 311 км. Эратосфен ошибся всего на 1 %: современное измерения для среднего радиуса Земли дают следующий результат: R3 = 6 371,03 км. В действительности Земля не является шаром, более точная модель «фигуры Земли» такая: сплюснутый эллипсоид вращения со средним экваториальным радиусом (большая полуось эллипсоида)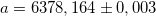 
км и полярным радиусом (меньшая ось эллипсоида) 
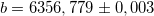км. Эксцентриситет этого эллипсоида вращения весьма невелик 
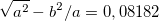, поэтому в большинстве задач Землю, с вполне достаточной точностью, можно считать шаром.
Схема опыта Эратосфена показана на рис. 5.6. В полдень в день летнего солнцестояния в городе Сиен (ныне Асуан) Солнце находилось в зените, и предметы не отбрасывали тени. В тот же день и в то же время в городе Александрия, находившемся в 5 000 стадиях от Сиена Солнце отклонялось от зенита примерно на 7°. Это составляет примерно 1/50 полного круга (360°), откуда получается, что окружность Земли равна 250 000 стадий.
Зная длину меридиана, можно узнать каким «стадием» пользовался Эратосфен, поскольку в древности в ходу были следующие стадии:
• вавилонский = 194 м
• греческий = 178 м
o аттический = 177,6 м
o олимпийский = 192,27 м
• египетский = 172,5 м
o стадий системы фараонов = 209,4 м
• птолемеевский и римский = 185 м
• стадий (гхальва) ассиро-халдейско-персидской системы = 230,4 м
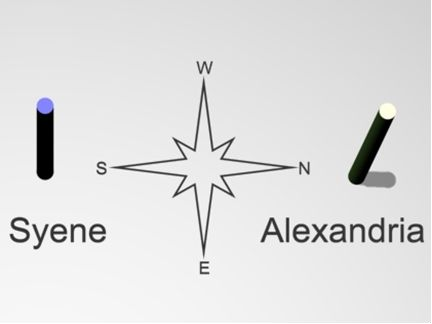
Рис. 5.6. Опыт Эратосфена по определению радиуса Земли
Как найти массу Земли? Каждое тело массой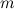 
притягивается к ней с силой
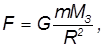
где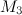 
— масса Земли, а 
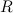— расстояние от тела до центра Земли. С другой стороны, отношение силы к массе — это ускорение свободного падения 
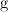(вращением Земли пренебрегаем):
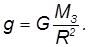
Отсюда следует, что 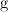не зависит от массы и размеров тела и определяется исключительно параметрами Земли и расстоянием до нее. Вблизи поверхности Земли
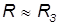
и 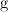= 9,81 м/с2. Находим отсюда массу Земли:
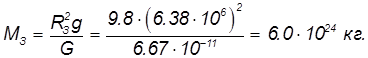
Ближайшим к Земле небесным телом является Луна. Определим расстояние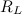 
до Луны. Мы знаем, что период обращения Луны вокруг Земли равен 
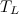= 27,32 сут = 27,32·86 400 = 2,36·106 с. Центростремительное ускорение Луны
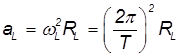
должно быть равно ускорению свободного падения на орбите Луны при 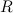= 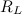. Приравнивая 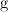и 
, находим:
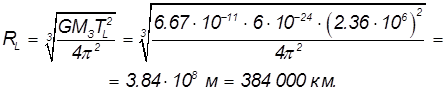
Скорость Луны на орбите равна
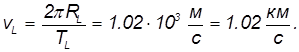
Легко определить угловой диаметр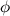 
Луны: большой палец, толщина которого примерно равна 1 см, закрывает при вытянутой руке (то есть на расстоянии примерно 1 м) ее диск. Отсюда
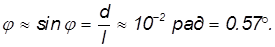
Более точные измерения дают для углового диаметра
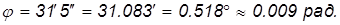
Отсюда радиус Луны будет
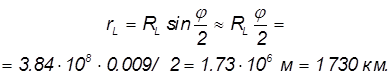
Зная расстояние от Земли до Луны, с помощью геометрии можно определить расстояние от Земли до Солнца. Когда Луна находится в первой четверти, направления от нее в сторону Земли и в сторону Солнца составляют прямой угол (рис. 5.7).
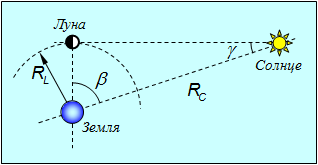
Рис. 5.7. Геометрический метод определения расстояния от Земли до Солнца
Если в этот момент на Земле измерить угол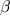 
между направлениями на Луну и Солнце, то расстояние до Солнца определится как
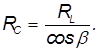
Угол 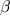оказывается близким к прямому: 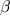= 89°51'. Поэтому удобнее будет пользоваться дополнительным углом 
= 
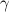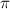/2 – β = 9' = 0,15° = 0,0026 рад. Тогда расстояние до Солнца будет равно
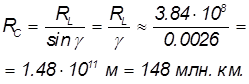
Это расстояние называется астрономической единицей (А или a.e., выше оно обозначено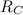 
). Более точно, A = 1,496·1011 м.
Зная период обращения Земли вокруг Солнца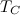 
= 1 год = 365,25 сут = 3,156·107 с, находим скорость Земли на орбите:
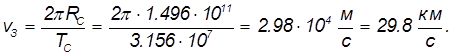
Наконец, мы определим параметры Солнца. Видимый с Земли угловой диаметр Солнца примерно таков же, как и у Луны: φ = 32' = 0,533° = 9,31·10–3 рад. Отсюда находим радиус Солнца:
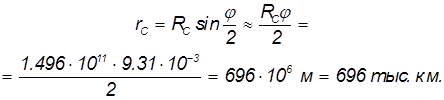
Массу Солнца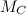 
получаем из закона всемирного тяготения: центростремительное ускорение Земли на орбите
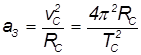
должно быть равно ускорению свободного падения Земли на Солнце
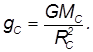
Приравнивая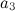 
и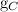 
, получаем:
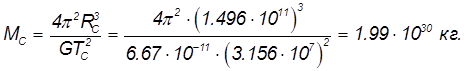
В этом выражении мы видим знакомую по третьему закону Кеплера комбинацию: отношение куба расстояния от планеты до Солнца к квадрату периода обращения. У всех планет это отношение одинаково, так как они вращаются вокруг одной и той же звезды.
Орбитальную скорость Земли можно также записать в виде
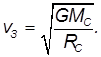
Это выражение справедливо для любой планеты при соответствующем изменении радиуса орбиты .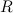
Приведенные оценки показывают, как много можно узнать о мире, наблюдая его из удобного кресла и ... понимая законы природы.
Дополнительная информация
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 41–42 (§ 4, задача 4): о скорости движения тени Луны по поверхности Земли во время полного солнечного затмения.
http://school-collection.edu.ru/catalog/res/e6609a18-088c-4979-83f0-faeeeef9faa1/?sort=order&from=ffb3b711-8f44-408c-aea4-a29842431067&&rubric_id%5B%5D=110200&rubric_id%5B%5D=110201 — Соросовский образовательный журнал, 1998 г., № 2 — анимация «Вращение Земли вокруг Солнца. День, ночь, времена года, фазы Луны».
http://www.somit.ru/fisika7_1.html — анимация, демонстрирующая причину смены дня и ночи на Земле и движение Луны.
