6.4. Постулаты Эйнштейна. Некоторые эффекты специальной теории относительности

Достижения предшественников были осмыслены и приведены в стройную систему благодаря работам А. Пуанкаре и А. Эйнштейна.

Рис. 6.5. А. Эйнштейн

К 1905 г. была создана специальная теория относительности. Специальная теория относительности (СТО) представляет собой современную физическую теорию пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно. СТО основана на двух постулатах.

Принцип относительности:

Принцип инвариантности скорости света:

Первый постулат является обобщением механического принципа относительности Галилея на все явления природы. Согласно второму постулату, постоянство скорости света — фундаментальное свойство природы, которое констатируется как опытный факт. Выше мы использовали этот постулат в форме уравнений движения светового импульса

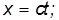
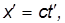
Из этих постулатов следует необходимость замены преобразований Галилея преобразованиями Лоренца.

Непосредственное следствие преобразований Лоренца: не может быть объектов, движущихся быстрее света. С такими объектами можно было бы связать систему отсчета, а при V > c для координат и времен получатся мнимые значения. Выходит, что скорость света играет роль предельно возможной скорости распространения сигнала.

Инвариантность интервала. Пусть даны два события: одно произошло в момент времени t₁ в точке с координатами x₁, y₁, z₁, а второе — в момент времени t₂ в точке с координатами x₂, y₂, z₂.

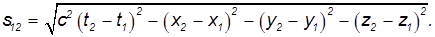
Поставив над координатами и временами штрихи, мы получим величину интервала s'₁₂ между этими же событиями в другой системе отсчета. Из преобразований Лоренца находим:

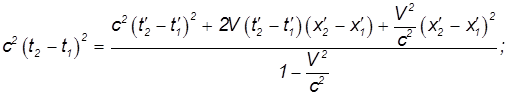
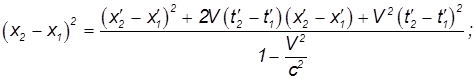
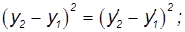
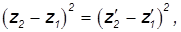
откуда следует:

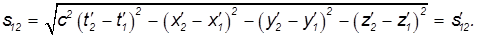
Таким образом,

В классической механике таким свойством обладали по отдельности временной интервал

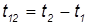
и пространственное расстояние

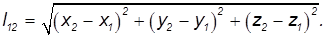
В релятивистской физике (от англ. relativity — относительность) этим свойством обладает только интервал между событиями

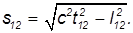
Замедление времени. Пусть в начале координат системы К' закреплены часы: их координаты равны тогда х' = у' = z' = 0, a t' — показываемое ими время (то есть время в системе отсчета К'). Подставляя эти значения в уравнения преобразований Лоренца, находим обычные выражения для координат этих часов в системе К: х = Vt, у = z = 0 (то есть в системе К часы движутся со скоростью V вдоль оси х). Удивительным является последнее уравнение — преобразование времени:

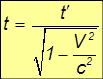
или

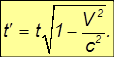
Время t', отсчитываемое часами в системе К', меньше времени t, отсчитываемого часами системы К.

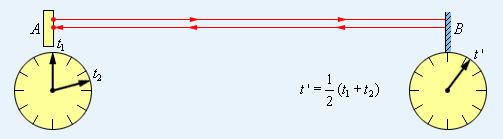
Рис. 6.6. Согласование показаний часов у наблюдателей А и В

Конкретное устройство часов здесь не играет никакой роли: речь идет о том, что временной интервал не является больше инвариантом и различен для разных систем отсчета. Это демонстрирует следующий пример.

Пример 1. Время жизни τ₀ покоящегося мюона (одной из элементарных частиц) равно 2,2 мкс. От точки рождения до детектора, зарегистрировавшего его распад, мюон пролетел расстояние l = 6 км. Определим, с какой скоростью v (в долях скорости света) летел мюон.

В системе отсчета К', связанной с мюоном, его время жизни равно τ₀. В лабораторной системе К, согласно полученному соотношению, от рождения мюона до распада пройдет время

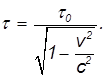
За это время мюон преодолеет расстояние

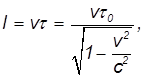
откуда находим

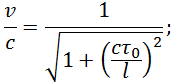
Величина

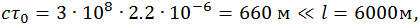
подставляя cτ₀ и l в (6.4.1), получаем

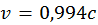
Если бы время жизни мюона относительно лабораторной системы К было таким же как и в той системе отсчета, где он покоится, то в лабораторной системе отсчета он пролетел бы расстояние L

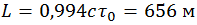
которое более чем в девять раз меньше действительного. Даже если бы он летел не со своей действительной скоростью (6.4.2), а с предельной скоростью c, что невозможно для частицы с отличной от нуля массой, он пролетел бы всего ct₀ = 660 м, но никак не 6 км.

Многочисленные наблюдения за элементарными частицами, покрывающими гораздо большие расстояния, чем им позволяет классическая механика, — прямое доказательство реальности эффекта замедления времени.

Рис. 6.7. Распад пи-мезона на мюон и нейтрино

Сокращение длины. Пусть в движущейся системе отсчета вдоль оси 0x закреплена линейка, длина которой (собственная длина) равна l₀. Если один конец линейки находится в начале координат (x'₁ = 0), а ее другой конец находится в точке с координатой x'₂=l₀, то из преобразований Лоренца непосредственно следуют координаты концов линейки в системе отсчета К :

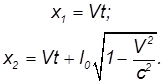
Разность этих координат дает длину линейки в системе отсчета К :

Движущаяся линейка становится короче линейки покоящейся. Этот факт также находится в согласии с утверждением, что в релятивистской механике инвариантом является интервал s₁₂, а не пространственные расстояния. Полученное сокращение длины движущегося объекта напоминает сокращение Фитцджеральда-Лоренца. Но с той разницей, что никакой эфир на объект не действует и никаких механических напряжений в линейке не возникает. Просто длина в движущейся и неподвижной системе отсчета различается, как различаются временные интервалы между двумя событиями. Эти оба эффекта — сокращение длины и замедление времени — связаны друг с другом.

Пример 2. Рассмотрим события, описанные в предыдущем примере, с точки зрения наблюдателя, «сидящего» на мюоне.

В момент рождения мюона детектор, регистрирующий его распад, находился с точки зрения наблюдателя в лаборатории на расстоянии l. С точки зрения наблюдателя на мюоне детектор приближается к мюону со скоростью v, причем начальное расстояние L до него будет меньше:

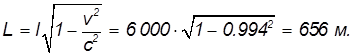
Детектор приблизится к мюону за время

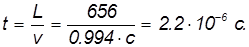
Это время совпадает со временем жизни мюона, который распадется в детекторе, как это видел и неподвижный наблюдатель. Описания событий разные, но оба наблюдателя зафиксируют один и тот же физический факт — распад мюона в детекторе.

Одновременность событий. Пусть имеются два события 1 и 2. Место и время совершения первого из них выберем за начало отсчета соответствующих координат: x₁ = 0, t₁ = 0. Пусть событие 2 происходит одновременно или позже первого

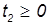
в точке на оси 0x, удаленной на расстояние L. Посмотрим, каковы координаты и моменты времени совершения этих событий с точки зрения наблюдателя, движущегося в положительном направлении оси 0x со скоростью V. Из преобразований Лоренца следует, что x'₁ = 0, t'₁ = 0, то есть координаты и время совершения первого события не изменяются. Второе же событие произойдет в точке x'₂ в момент времени t'₂, где

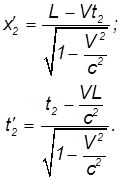
Знак координаты x'₂ будет таким же, как и в классической механике. Если наблюдатель не успеет долететь до места совершения события к моменту, когда оно произойдет (Vt₂ < L), то событие случится у него впереди по курсу (x'₂ > 0), если же успеет (Vt₂ > L), — то событие 2 произойдет сзади него (x'₂ < 0). Но вот то, что происходит с моментом совершения события 2, не имеет аналога в классической физике. В самом деле, относительно неподвижного наблюдателя событие 2 произошло позже события 1. Но при достаточно большой скорости

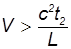
знак у t'₂ становится отрицательным, то есть порядок событий меняется!

Но всегда ли это возможно? Ведь события 1 и 2 могут быть причинно связаны друг с другом. Например, событие 1 — рождения отца, а событие 2 — рождение его ребенка. Разве не было бы абсурдным, если бы нашелся наблюдатель, для которого ребенок родился бы прежде отца (нарушилась бы, как говорят, причинно-следственная связь)? Конечно, это невозможно. Давайте сформулируем условие, при котором события 1 и 2 могут быть связаны друг с другом. Так как максимально возможная скорость распространения любого сигнала не превышает c, то события могут находиться в причинно-следственной связи, если они не слишком удалены друг от друга:

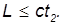
Только тогда «сообщение» о первом событии достигнет второго до его совершения. Но если

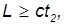
то для изменения порядка событий наблюдатель должен двигаться со скоростью

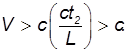
А это, как мы видели, невозможно.

Таким образом, события, которые могут в принципе зависеть друг от друга, имеют тот же временной порядок для всех наблюдателей.

Если же события происходят настолько далеко друг от друга, что они не могут быть связаны никаким сигналом

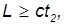
то порядок совершения этих событий зависит от скорости движения наблюдателя и при

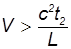
порядок событий будет иным, нежели в неподвижной системе отсчета. В частности, одновременные события (t₁ = t₂), происходящие в неподвижной системе отсчета на любом расстоянии друг от друга, не могут быть причинно-связанными (для этого нужны были бы сигналы с бесконечно большой скоростью). Из формулы для преобразования времени получаем при t₂ = 0:

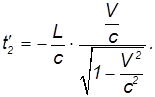
Значит, при любой скорости наблюдателя, движущегося в положительном направлении оси 0x, событие 2 происходит раньше события 1. При движении в обратном направлении (V < 0) событие 2 происходит позже.

Рис. 6.8. События могут быть одновременными, с точки зрения некоего наблюдателя, если ds² > 0

Проиллюстрируем сказанное на следующем примере. Пусть движется поезд А’В’, в концы которого ударяют две молнии, оставляющее на рельсах отметки А и В (рис. 6.9).

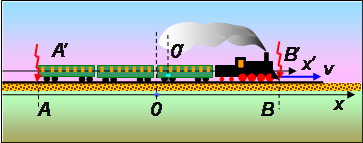
Рис. 6.9. К понятию относительности одновременности

Отметим в поезде среднюю точку 0’, а на полотне — соответственно 0. Свяжем с железнодорожным полотном систему отсчета 0х, а с поездом — систему отсчета 0х’. Пусть в точку 0 вспышки света происходят одновременно. Тогда в неподвижной системе отсчета х оба события (удары молнии) происходят одновременно.

Поскольку поезд движется вправо, и, следовательно, в момент прихода вспышек в середину поезда точка 0’ находится правее 0, то вспышка из точки А’ в точку 0’ придет позже, чем из точки B'. Это означает, что в системе х’ удар молнии в точке В’ происходит раньше, чем в точке А’.

Мы убедились, что наряду с относительностью временных интервалов и пространственных расстояний даже одновременность событий не имеет абсолютного значения. Все они относительны, то есть зависят от движения наблюдателя. В классической физике относительными были, например, скорости тел, их кинетические энергии. Теперь список подобных величин пополнился, только и всего.

Рис. 6.10. Кинематические преобразования физических величин в СТО