ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
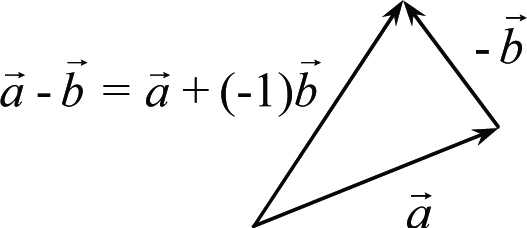
Рис. 1.6
называется вектор 
. Это значит, что для того чтобы найти разность надо к вектору 
прибавить вектор, противоположный вектору 
. Вычитание векторов и , которые использовались во всех предыдущих примерах, выполнено на рис. 1.6.Из данных выше определений суммы и разности векторов следует, что при сложении и вычитании векторов их модули, вообще говоря, не складываются и не вычитаются. Действительно, векторы слагаемые и вектор сумма образуют треугольник, а в треугольнике длина любой стороны меньше суммы длин двух других сторон, но больше их разности. Поэтому, если для трех векторов выполняется равенство 
, то для их модулей справедливы неравенства 
, причем равенства здесь имеют место только в том случае, когда векторы и одинаково или противоположно направлены. Рассмотрим пример.
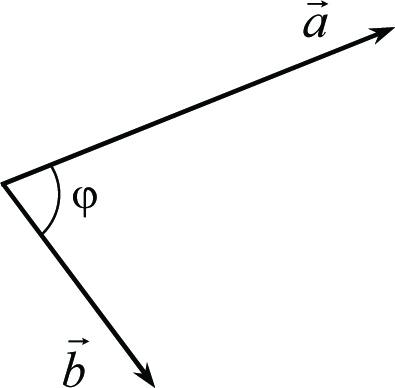
Рис. 1.7
Пример 1.11. Даны векторы и , угол между которыми равен 
(рис. 1.7). Найти модуль векторов 
и .
Решение. Сумма данных в условии векторов и найдена на рис. 1.8 по правилу треугольника. Для нахождения модуля вектора найдем длину стороны AB в треугольнике векторного сложения ABC (рис. 1.8). Так как 
, то 
в треугольнике векторного сложения равен 
.
1 Задачи, рассматриваемые в качестве примеров, набраны курсивом.
