ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
Поэтому из теоремы косинусов для треугольника ABC имеем
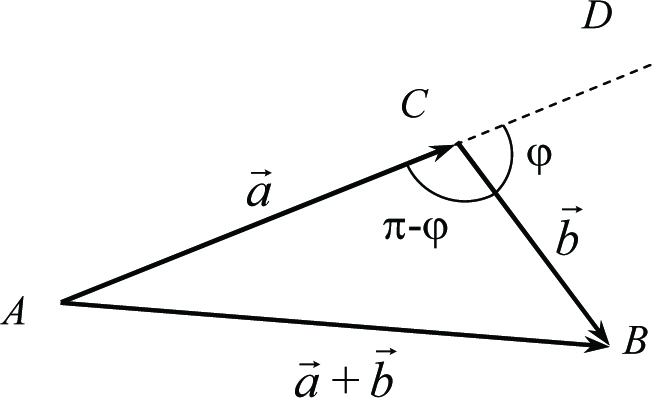
Рис. 1.8
Поскольку 
и 
, из формулы (1.1) получаем
Из формулы (1.2) следует, что модуль суммы двух векторов зависит не только от модулей векторов слагаемых, но и от угла между ними. Если векторы 
и 
направлены одинаково (
= 0), для модуля их суммы получаем из (1.2)
Для модуля суммы противоположно направленных векторов (
) формула (1.2) дает
(модуль в правой части формулы (1.4) – это модуль числа, а не вектора).
Аналогичное геометрическое рассмотрение модуля разности векторов приводит к соотношению
(предлагаем читателю получить это соотношение самостоятельно с помощью теоремы косинусов).
Простейшие свойства векторных операций. Данные выше правила сложения, вычитания и умножения векторов на числа обладают рядом тех же свойств, что и операции с числами.
