ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
В частности:
(1) 
. Это свойство называется переместительностью (или коммутативностью) правила сложения векторов.
(2) 
. Сочетательность (или ассоциативность) сложения.
(3) 
. Распределительность (или дистрибутивность) умножения векторов на числа.
(4) из равенства 
следует, что 
и 
.
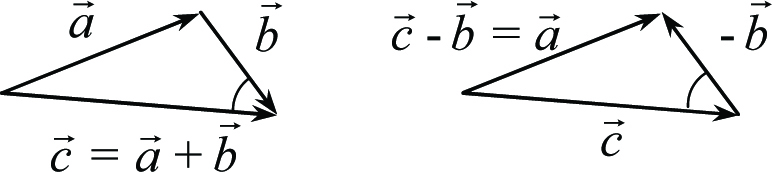
Рис. 1.9
Конечно, справедливость этих свойств вовсе не следует из того, что они справедливы для сложения и умножения чисел. Ведь правила действия с числами отличаются от правил действия с векторами. Перечисленные свойства векторных операций можно строго доказать на основе определений сложения векторов и умножения векторов на числа. Докажем, например, правило (4). Для этого рассмотрим два произвольных вектора 
и 
и найдем вектор их суммы 
. Это построение выполнено в левой части рис. 1.9.
Теперь найдем разность 
− и докажем, что этот вектор равен вектору . Согласно определению для нахождения разности надо к вектору прибавить вектор −. Это построение выполнено на правом рис. 1.9. Очевидно, два треугольника векторного сложения на рис. 1.9. равны. Действительно, в этих треугольниках равны друг другу длины сторон, представленных векторами , и векторами и − (поскольку модули последних векторов совпадают), а также угол между этими сторонами (поскольку стороны, представленные векторами и − параллельны друг другу; этот угол отмечен на рисунке). Поэтому в этих треугольниках равны и третьи стороны, то есть 
.
