ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
Векторы, параллельные одной и той же прямой, называются коллинеарными. Векторы, параллельные одной и той же плоскости, называются компланарными.
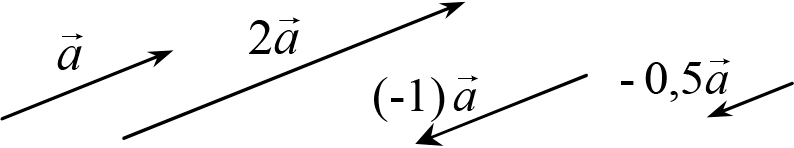
Рис. 1.3
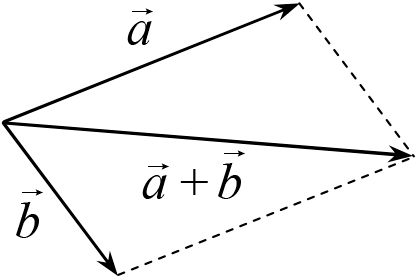
Рис. 1.4
Как указывалось выше, суммой векторов ![]() и
и ![]() называется вектор, который обозначается
называется вектор, который обозначается ![]() и находится геометрически по правилу параллелограмма: вектор
и находится геометрически по правилу параллелограмма: вектор ![]() нужно
перенести, оставляя его параллельным самому себе, так, чтобы его начало совпало с началом вектора
нужно
перенести, оставляя его параллельным самому себе, так, чтобы его начало совпало с началом вектора ![]() , построить на векторах
, построить на векторах ![]() и
и ![]() параллелограмм, вектор суммы
параллелограмм, вектор суммы ![]() будет направлен по диагонали этого параллелограмма из той точки, где находятся начала векторов
будет направлен по диагонали этого параллелограмма из той точки, где находятся начала векторов ![]() и
и ![]() (рис. 1.4).
(рис. 1.4).
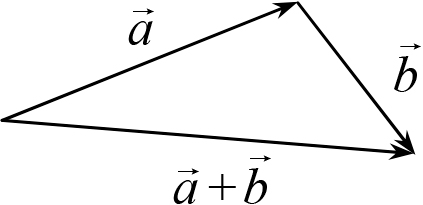
Рис. 1.5
Правило векторного сложения может быть сформулировано и по-другому. Чтобы найти вектор суммы ![]() вектор
вектор ![]() нужно перенести, оставляя его параллельным самому себе, так, чтобы его начало совпало с концом вектора
нужно перенести, оставляя его параллельным самому себе, так, чтобы его начало совпало с концом вектора ![]() ; вектор суммы будет направлен из начала вектора
; вектор суммы будет направлен из начала вектора ![]() в конец вектора
в конец вектора ![]() . Правило векторного сложения в такой формулировке называется правилом треугольника. Суммирование тех же векторов, что и на рис. 1.4, с помощью правила треугольника выполнено на рис. 1.5. Очевидно, правила параллелограмма и треугольника эквивалентны. Действительно, «верхняя часть» параллелограмма на рис. 1.4 представляет собой тот же треугольник, что получается при использовании правила треугольника на рис. 1.5, то есть эти правила приводят к одному и тому же вектору суммы. Поэтому для суммирования векторов может быть использовано любое из них.
. Правило векторного сложения в такой формулировке называется правилом треугольника. Суммирование тех же векторов, что и на рис. 1.4, с помощью правила треугольника выполнено на рис. 1.5. Очевидно, правила параллелограмма и треугольника эквивалентны. Действительно, «верхняя часть» параллелограмма на рис. 1.4 представляет собой тот же треугольник, что получается при использовании правила треугольника на рис. 1.5, то есть эти правила приводят к одному и тому же вектору суммы. Поэтому для суммирования векторов может быть использовано любое из них.


