ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
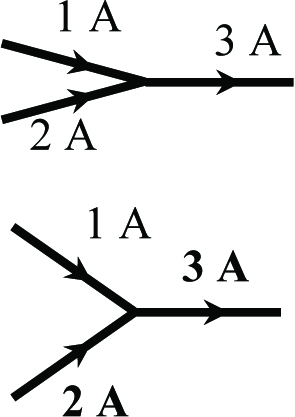
Рис. 1.2
Действительно, силу тока можно было бы считать вектором, направленным вдоль провода, с модулем, равным величине силы тока, если бы при соединении проводов токи складывались по правилу векторного сложения. Однако независимо от направлений проводов, входящих в точку соединения, при силах тока в них 1 и 2 Ампера ток в выходящем проводе будет равен 3 Ампера (рис. 1.2). Это значит, что токи складываются как числа, и, следовательно, мы должны считать силу тока скаляром.
Для работы с векторными физическими величинами разработан специальный математический аппарат, который называется векторной алгеброй и широко используется в физике. Дадим краткий обзор этого математического аппарата, отвлекаясь пока от его физических приложений.
Основные определения. Векторы изображаются направленными отрезками и обозначаются буквами со стрелками над ними 
, 
, ... или жирными буквами a, b, …; первое обозначение используется в настоящей книге. Два вектора и считаются равными = , если они имеют одинаковую длину и одинаково направлены. Длину вектора называют также его модулем (или абсолютной величиной) и обозначают || , ||, … или соответствующей нежирной буквой без стрелки a, b ... Модуль любого вектора является величиной неотрицательной.
Векторы можно умножать на числа и складывать друг с другом. Произведением вектора на число λ называется вектор, который обозначается λ и определяется следующим образом: вектор λ направлен так же, как и вектор , если λ > 0, и противоположно, если λ < 0; модуль вектора λ равен |λ|||, то есть |λ|=|λ|||.
На рис. 1.3. выполнено умножение некоторого вектора на ряд чисел. Отметим, что вектор (−1), который направлен противоположно вектору и равен ему по модулю, называется вектором, противоположным вектору и часто обозначается просто −.
