ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
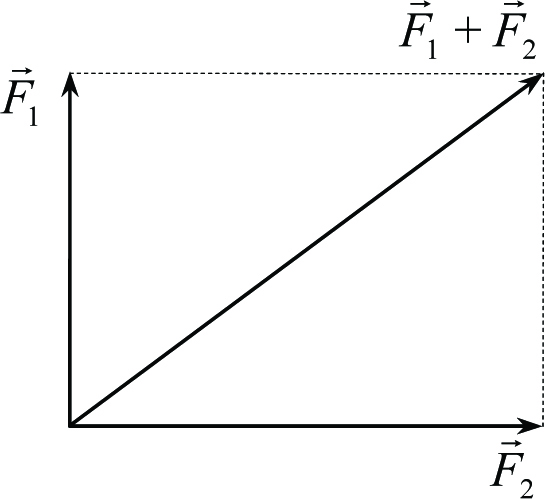
Рис. 1.1
описывающий движение тела под действием нескольких сил, фактически, задает нам правило сложения сил, которое называется правилом параллелограмма. Величины, которые обладают такими свойствами, то есть характеризуются численным значением и направлением в пространстве и складываются с себе подобными величинами по правилу параллелограмма (или треугольника – другой вариант правила сложения векторов), называются векторными или векторами. Среди физических величин, рассматриваемых в школьном курсе физики, к векторным относятся: скорость, сила, импульс, напряженность электрического поля и др.
Понятие вектора ввел в математику выдающийся ирландский математик и физик У. Гамильтон (1805 —1865). Он сформулировал основы векторного исчисления, описал некоторые операции векторного анализа. Гамильтон является и автором самого термина «вектор» (лат. vector – несущий). В последующем векторный анализ использовал Дж. Максвелл в своих трудах по электромагнетизму, обратив внимание физиков на новое исчисление. Развил векторный анализ Дж. Гиббс, а затем О. Хевисайд в начале двадцатого века придал ему современный вид, в том числе и с точки зрения обозначений.
Последний пункт определения векторной величины является очень существенным. Например, силу или скорость можно считать векторами, а силу тока или кинетическую энергию – нельзя, несмотря на то, что последние величины и можно было бы охарактеризовать определенным направлением1.
1 См. также обсуждение этого вопроса в очень глубокой книге С.В. Ащеулова и В.А. Барышева «Задачи по элементарной физике».


