ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
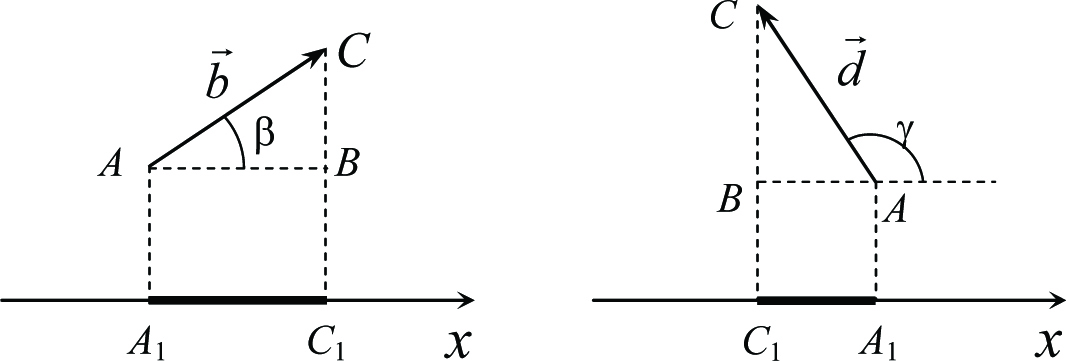
Рис. 1.11
Для нахождения проекций векторов удобно использовать следующие геометрические соображения. Рассмотрим вектор ![]() , образующий острый угол с осью (левая часть рис. 1.11). Опустим перпендикуляры AA1 и CC1 из начала и конца вектора на числовую ось и построим отрезок AB, параллельный оси. Из прямоугольного треугольника ABC нетрудно видеть, что произведение bcos β (то есть проекция вектора на ось x) имеет смысл длины катета AB. Поэтому проекция вектора
, образующий острый угол с осью (левая часть рис. 1.11). Опустим перпендикуляры AA1 и CC1 из начала и конца вектора на числовую ось и построим отрезок AB, параллельный оси. Из прямоугольного треугольника ABC нетрудно видеть, что произведение bcos β (то есть проекция вектора на ось x) имеет смысл длины катета AB. Поэтому проекция вектора ![]() на ось x равна длине отрезка AB или равного ему отрезка A1C1 между проекциями начала и конца вектора на ось (на рисунке этот отрезок числовой оси выделен жирным). Аналогичное рассмотрение вектора, составляющего тупой угол с осью, показывает (правая часть рис. 1.11), что проекция такого вектора на ось dcos γ = −dcos (π − γ) равна «минус» длине отрезка между проекциями его начала и конца на ось, т.е. минус длине отрезка C1A1 в правой части рис. 1.11.
на ось x равна длине отрезка AB или равного ему отрезка A1C1 между проекциями начала и конца вектора на ось (на рисунке этот отрезок числовой оси выделен жирным). Аналогичное рассмотрение вектора, составляющего тупой угол с осью, показывает (правая часть рис. 1.11), что проекция такого вектора на ось dcos γ = −dcos (π − γ) равна «минус» длине отрезка между проекциями его начала и конца на ось, т.е. минус длине отрезка C1A1 в правой части рис. 1.11.
Первое означает, что проекция вектора λ![]() на произвольную ось x равна произведению числа λ на проекцию вектора
на произвольную ось x равна произведению числа λ на проекцию вектора ![]() на эту ось, второе – что проекция вектора суммы двух векторов равна сумме проекций векторов-слагаемых.
на эту ось, второе – что проекция вектора суммы двух векторов равна сумме проекций векторов-слагаемых.


