ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ
Соотношения (1.7), (1.8) непосредственно следуют из определений произведения вектора на число, суммы векторов и проекции вектора на ось и иллюстрируются рис. 1.12, который не требует особых комментариев. Отметим только, что эти соотношения справедливы независимо от знаков числа λ и проекций входящих в них векторов. Предлагаем читателю убедиться в этом самостоятельно, рассмотрев несколько соответствующих примеров.
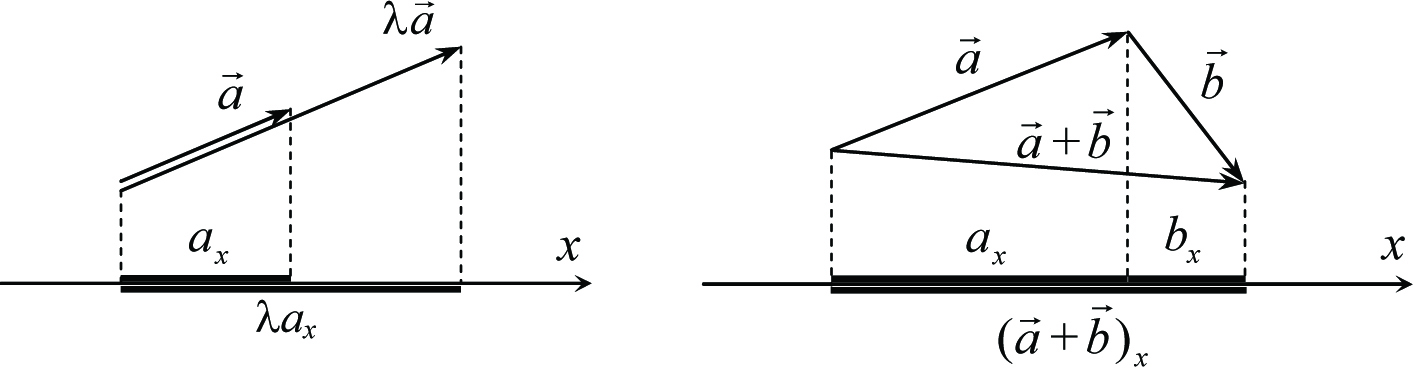
Рис. 1.12
Соотношения (1.7), (1.8) широко используются при решении физических задач. Дело в том, что целый ряд законов физики являются векторными (к таким законам относятся, например, законы равноускоренного движения, второй закон Ньютона, закон сохранения импульса и др.). То есть эти законы связывают векторные физические величины, и действия, использующиеся в них, являются действиями с векторами. Поэтому для того, чтобы найти какую-то из величин, входящих в такой закон необходимо провести определенные вычисления с векторами: сложение, вычитание, умножение на числа. С другой стороны, если какой-то вектор равен сумме двух (или более) векторов, то согласно (1.8) его проекция на любую числовую ось равна сумме проекций векторов слагаемых. Таким образом, закон, связывающий векторы, дает также связь между проекциями этих векторов на числовые оси. Это значит, что любое векторное равенство эквивалентно числовым равенствам для проекций векторов на координатные оси, причем в последних используются действия с числами. Можно сказать, что такой переход к уравнениям для проекций является простым способом «перевода» геометрического языка векторных законов на алгебраический язык, который, как правило, является более простым, так как использует действия с числами.


