ГЛАВА 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
где 
– скорость тела спустя еще один интервал времени τ. Складывая найденный в предыдущем пункте вектор импульса силы с вектором 
, находим вектор 
(рис. 9.1 б). Величину вектора и угол между этим вектором и вектором, например, 
можно найти из треугольника векторного сложения. По теореме косинусов имеем
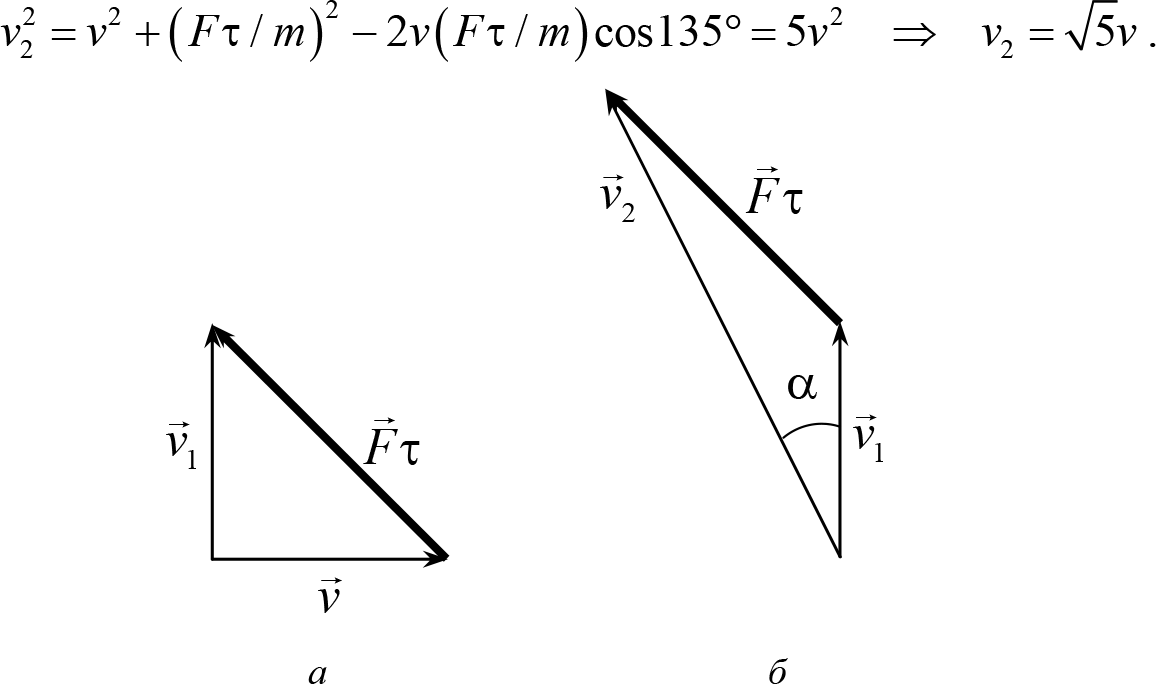
Рис. 9.1
Угол между вектором и вектором проще всего найти из
теоремы синусов (на рис. 9.1 этот угол обозначен как α). Из треугольника векторного сложения получаем
Докажем теперь, что импульс замкнутой системы тел не изменяется независимо от того, как взаимодействуют тела внутри системы. Для этого рассмотрим замкнутую систему из двух тел с массами m1 и m2 (два – для простоты; вывод легко обобщается на случай произвольного количества тел). Пусть в некоторый момент
времени скорости тел равны и . Скорости тел спустя бесконечно малый интервал времени 
и 
найдем по второму закону Ньютона для рассматриваемых тел
