ГЛАВА 11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ И ИЗМЕНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
А поскольку рассматриваемый участок траектории произволен, из формулы (11.10) заключаем, что сумма кинетической и потенциальной энергий тела E = K + Π остается неизменной в процессе движения, или, как говорят, сохраняется. Эта величина E называется механической энергией тела, а утверждение о ее сохранении - законом сохранения механической энергии.
Соотношение (11.10) можно использовать для нахождения скорости тела в той или иной точке (эта скорость входит в (11.10) через кинетическую энергию), или каких-либо пройденных телам расстояний, которые входят в (11.10) через потенциальную энергию. Рассмотрим пример.
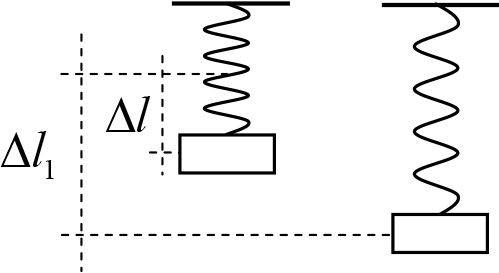
Рис. 11.4
Пример 11.1. Груз массой m подвешен к свободному концу висящей невесомой пружины с коэффициентом жесткости k. В начальный момент груз удерживают так, что пружина растянута на величину Δl по сравнению со своим недеформированным состоянием. Груз отпускают, и он начинает опускаться. Найти максимальное удлинение пружины в процессе последующего движения (рис. 11.4.).
Решение. Так как после освобождения груз начинает опускаться, сила упругости, действующая на груз в начальном положении, меньше его силы тяжести. Пусть максимальное удлинение пружины по сравнению с недеформированном состоянием равно Δl1 (см. рис. 11.4). Для нахождения этой величины применим к движению тела от начального положения до положения, в котором пружина будет растянута на максимальную величину, закон сохранения механической энергии. Полная механическая энергия тела складывается из его кинетической энергии, потенциальной энергии тела в поле силы тяжести и потенциальной энергии растянутой пружины.
Выберем за начало отсчета потенциальной энергии пружины ее недеформированное положение, тяжести – положение тела в момент максимального растяжения пружины.


