ГЛАВА 11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ И ИЗМЕНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Используя далее связь работы потенциальных сил с потенциальной энергией, получим
или
Из формулы (11.16) следует, что в присутствии непотенциальных сил механическая энергия тела изменяется, и это изменение равно работе действующих на тело непотенциальных сил. Утверждение (11.16) может быть названо законом изменения механической энергии в присутствии непотенциальных сил. Использование этого закона для решения задач, как правило, не вызывает трудностей. Нужно понять, какие потенциальные и какие непотенциальные силы действуют на тело, каковы потенциальные энергии потенциальных сил и работы непотенциальных. После этого составляется уравнение закона (11.16), из которого находится неизвестная величина. Рассмотрим пример.
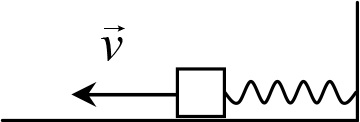
Рис. 11.5
Решение. Применим к движению тела от толчка до остановки закон изменения механической энергии. Начальная энергия системы (в момент толчка) – кинетическая энергия тела mv2 / 2, конечная (в момент остановки тела) – потенциальная энергия пружины kΔx2 / 2(Δx – максимальное растяжение пружины). Поскольку в системе действуют силы трения, ее механическая энергия не сохраняется: изменение механической энергии системы равняется работе силы трения. Поэтому имеем
где A = −μmgΔx – работа силы трения, совершенная над телом при его перемещении на величину Δx. Решая квадратное уравнение (11.17), находим


