ГЛАВА 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. МЕТОД КООРДИНАТ В МЕХАНИКЕ

Какова траектория середины стержня С? Найти зависимости координат точек A, B и C от времени.

Решение. Согласно логике Декарта для описания движения любого тела (в нашем случае это точки A, B и C) необходимо найти зависимости их координат от времени, а затем исследовать эти функции.

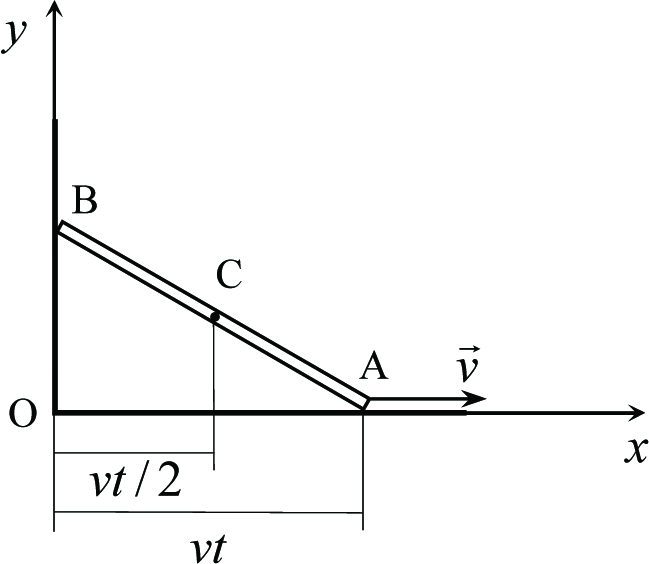
Рис. 1.15

Поскольку точка A находится все время на горизонтальной опоре, ее y - координата в любой момент времени равна нулю y_A(t) = 0, а x - координата равна длине отрезка OA (рис. 1.15). Поскольку точка A движется равномерно и в начальный момент находилась в точке O, то за время t после начала движения она проходит путь OA = vt. Поэтому x_A(t) = vt. Итак, для точки А имеем

Для точки В ситуация обратная: в любой момент времени ее x координата равна нулю, y -координату точки B можно найти по теореме Пифагора из прямоугольного треугольника ОАВ:

где l – длина стержня.

Для нахождения зависимостей координат точки C от времени заметим, что ее координаты в любой момент времени равно вдвое меньше соответствующих координат точек A и B. Поэтому

Чтобы получить уравнение траектории точки С необходимо из двух предыдущих формул исключить время, то есть получить зависимость ее y-координаты в любой момент времени от ее x-координаты в этот момент. Для этого выразим время через x-координату и подставим это выражение в формулу для y-координаты.

18/597