ГЛАВА 11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ И ИЗМЕНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ

где и – скорости шаров после столкновения (рис. 11.7, на 12 котором вектор скорости первого шара после столкновения v₁ мы изобразили направленным в ту же сторону, что и его скорость до удара; этот результат совсем неочевиден и должен быть проверен при решении). После сокращения массы и проецирования первого уравнения (11.23) на ось x, направленную вдоль движения шаров (см. рисунок), получим

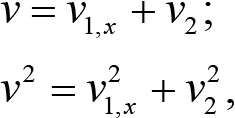
где v_1,x – проекция скорости первого шара после столкновения на ось x. Решение системы уравнений (11.24) дает два набора корней

Очевидно, первый набор корней отвечает начальному движению, то есть отсутствию столкновения. (Отметим, что такая ситуация всегда имеет место при использовании законов сохранения. Один набор решений всегда должен дать начальное состояние, поскольку сохранение начальных скоростей законам сохранения и импульса удовлетворяет). Поэтому столкновению тел отвечает второй набор решений: то тело, которое двигалось первоначально, после центрального столкновения покоится, то тело, которое покоилось, движется с той же скоростью, что первое до столкновения.

Аналогичным образом можно доказать, что если до столкновения двигались бы оба тела, то в результате центрального упругого столкновения они также обменялись бы скоростями, как и в рассмотренном примере, в котором движется только одно из них. Однако если бы тела имели разные массы, такой результат не имел бы места.

Пример 11.5. Два тела массами m₁ и m₂ движутся навстречу друг другу со скоростями и соответственно. Происходит центральное, абсолютно неупругое столкновение. Найти количество выделившегося при этом тепла.

Решение. Согласно определению столкновение тел является абсолютно неупругим, если в процессе столкновения в тепло переходит максимально возможная доля механической энергии системы.