ГЛАВА 12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ. КИНЕМАТИКА И ДИНАМИКА
где T – время полного оборота или период движения (конечно, формула (12.6) справедлива для движения с постоянной угловой скоростью, которое только и рассматривается в настоящей книге). Из соотношения (12.6) следует, что для тел, вращающихся с известным периодом, угловая скорость, фактически, известна. Например, угловые скорости секундной, минутной и часовой стрелок часов равны, соответственно,
![]()
Заметим также, что угловые скорости стрелок любых часов одинаковы: например, минутные стрелки наручных часов и часов Спасской башни московского Кремля совершают полный оборот за 1 ч, и следовательно, имеют одинаковые угловые скорости. С угловой скоростью можно работать так же, как и с линейной скоростью; но если линейная скорость позволяет находить пройденные телом расстояния, то угловая - углы поворота тела за любые интервалы времени. Рассмотрим следующий пример.
Пример 12.2. На часах 16 ч. Через какое минимальное время после этого часовая и минутная стрелка встретятся?
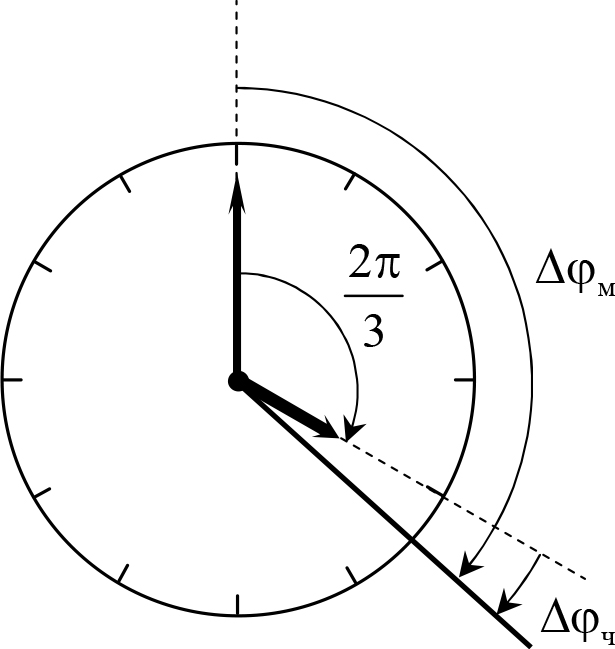
Рис. 12.2
Решение. Напомним, что при решении задачи о «линейном» движении тел друг за другом обычно рассуждают так (см. пример 1.2). Вводят неизвестное время встречи тел, через него (по формуле, связывающей расстояние, время и скорость) находят пути, пройденные каждым телом до встречи; разность этих путей очевидно равна первоначальному расстоянию между телами. Давайте попробуем использовать эти же рассуждения, но для случая угловых перемещений.


