ГЛАВА 12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ. КИНЕМАТИКА И ДИНАМИКА

Итак, пусть стрелки встретятся через время t после 16 ч. Тогда минутная стрелка повернется за это время на угол Δφ_м = ω_мt, часовая – на угол Δφ_ч = ω_чt (напомним, что угловые скорости ω_м и ω_ч нам известны, поскольку известны периоды вращения стрелок). Очевидно, разность углов поворота до встречи равна первоначальному углу между стрелками, который в начальный момент времени (в 16 ч) равен третьей части полного угла, т.е. 2π / 3 (рис. 12.2; место стрелок часов показано жирным сплошным отрезком). Поэтому уравнение, из которого можно найти время встречи, таково

Решая уравнение (12.8), находим

Для упрощения вычислений ответ (12.9) удобнее выразить через периоды вращения стрелок. Так как

то

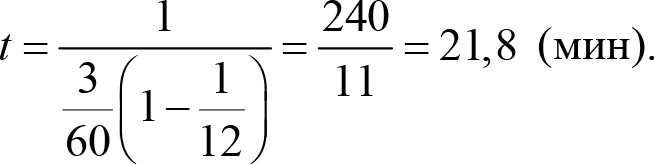
(Чтобы сделать поменьше числа и таким образом немножко упростить вычисления, мы выразили угловые скорости стрелок не в обратных секундах, а в обратных минутах, поэтому и ответ получили в минутах).

Рассмотрим теперь вопрос об ускорении тела при движении по окружности. Очевидно, что даже в случае движения с постоянной по величине скоростью ускорение тела не равно нулю, поскольку изменяется направление скорости, и вектор