ГЛАВА 13. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ

Ньютон написал, что идея закона обратных квадратов принадлежит, помимо него самого, также Э.Галлею (на его деньги издавались «Начала»), К. Рену (президенту Королевского общества) и Гуку. Галлей и Рен особого отношения к закону не имели, но против упоминания своих имен в таком контексте возражать не стали. В результате Гук оказался в числе людей, никак с законом всемирного тяготения не связанных. Гук после ознакомления с рукописью «Начал» был поражен отсутствием упоминания своего вклада в формулировку закона и обвинил Ньютона в краже своих идей. Не спасла положение и неуклюжая ссылка Ньютона на Гука, сделанная под нажимом Галлея. До самой своей смерти Гук боролся за свои права, но тщетно.

О вкладах Ньютона и Гука в формулировку закона прекрасно сказал исследователь творчества Ньютона академик С.И. Вавилов: «Если связать в одно все предположения и мысли Гука о движении планет и тяготении, высказанные им в течение почти 20 лет, то мы встретим почти все главные выводы «Начал» Ньютона, только высказанные в неуверенной и малодоказательной форме. Не решая задачи, Гук нашел ее ответ. Вместе с тем перед нами вовсе не случайно брошенная мысль, но несомненно плод долголетней работы. У Гука была гениальная догадка физика-экспериментатора, прозревающего в лабиринте фактов истинные соотношения и законы природы ... Гук не мог идти прямой, безукоризненной дорогой «Математических начал» Ньютона, но своими окольными тропинками, следов которых нам теперь уже не найти, он пришел туда же».

Для определения n нужно было сравнить силы притяжения, действующие со стороны Земли на тела, находящиеся от Земли на разных расстояниях. Но подъем тел над поверхностью на «человеческие» расстояния в несколько километров меняет расстояние от этих тел до центра Земли (и соответственно силу их притяжения к Земле) крайне незначительно, и заметить это изменение экспериментально во времена Ньютона было невозможно. Поэтому нужно было искать тела, находящиеся на существенно других расстояниях от Земли. К счастью для Ньютона одно такое тело существует — это Луна. Луна совершает круговое движение вокруг Земли и имеет центростремительное ускорение, которое обеспечивается гравитационной силой. Ускорение Луны a удобно выразить через период ее обращения T и радиус орбиты r

(13.3)

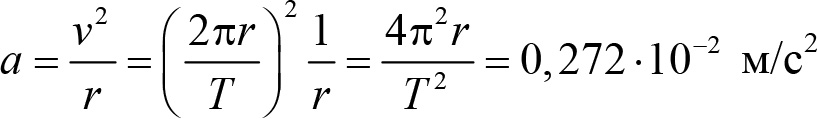
(здесь использованы известные значения периода обращения Луны вокруг Земли T = 27,3 суток и расстояния от Луны до Земли м. С другой стороны из закона (13.2) следует, что