ГЛАВА 13. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ

где — скорость вращающегося тела; r — радиус орбиты. Из формулы (13.11) видим, что скорость спутника и радиус его орбиты однозначно связаны друг с другом¹. Из формулы (13.11) получаем:

(13.12)

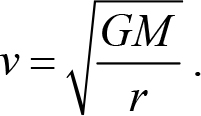
Если радиус орбиты спутника совпадает с радиусом планеты, то скорость (13.12) называется первой космической скоростью. Для Земли соотношение (13.12) дает = 7,9 км/с. Из (13.12) легко получить третий закон Кеплера.

Пример 13.2. Вокруг некоторой звезды вращаются планеты. Доказать, что отношение квадрата периода к кубу радиуса орбиты одинаково для всех планет (третий закон Кеплера). Орбиты планет круговые.

Решение. Из соотношения (13.12) находим период обращения T планеты вокруг звезды

(13.13)

где M — масса звезды; r — радиус орбиты планеты. Возводя равенство (13.13) в квадрат, получим

(13.14)

В левую часть формулы (13.14) входят характеристики каждой планеты — период ее обращения и радиус орбиты, в правую — только постоянные и масса звезды, вокруг которой планеты вращаются. А это значит, что отношение квадрата периода к кубу радиуса орбиты одинаково у всех планет, вращающихся вокруг данной звезды.

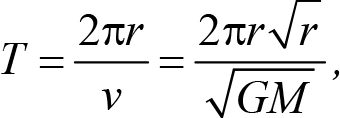
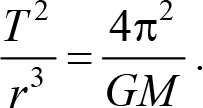
¹ Речь, конечно, идет о движении только под действием гравитационной силы. Если кроме силы гравитации на тело действуют другие силы, например, работающий двигатель на космический корабль, скорость этого тела не обязана быть связана с радиусом орбиты выражением (13.11).

208/597