ГЛАВА 13. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
то r → ∞, и, следовательно, тело может покинуть область притяжения планеты. Скорость (13.21) называется второй космической скоростью. Для Земли она составляет ν = 11,1 км/с. Если в начальный момент тело имеет скорость, которая больше второй космической, то при покидании области притяжения планеты оно будет иметь некоторую скорость, которую также можно найти из закона сохранения энергии.
Если необходимо найти силы взаимодействия нескольких (более двух) точечных тел используются закон всемирного тяготения и принцип суперпозиции сил, который утверждает, что силу, действующую на тело m1 в системе из трех тел, можно найти следующим образом1.
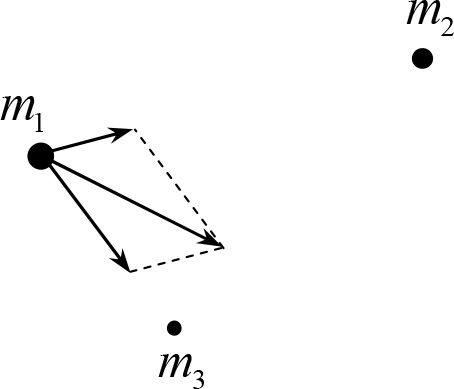
Рис. 13.1
Сначала необходимо найти силу, действующую на тело m1 со стороны тела m2 (по закону всемирного тяготения, фактически, считая, что тело m3 никак не «мешает» взаимодействовать телам m1 и m2). Затем точно так же нужно найти силу, действующую на тело m1 со стороны тела m3. Результирующая сила будет равна векторной сумме этих сил (рис. 13.1). Точно таким же способом можно найти и силы, действующие в этой системе на другие тела (соответствующие векторы на рисунке не показаны).
Принцип суперпозиции дает метод вычисления сил гравитации, действующих между неточными телами. Этот метод заключается в том, протяженное тело мысленно делится на малые части, которые можно считать точечными, а затем по закону всемирного тяготения находятся силы взаимодействия каждой пары точечных частей. Суммарная сила, действующая на одно из тел, есть векторная сумма сил, действующих на каждую его малую часть со стороны малых частей другого тела.
1 В школьном курсе физики принцип суперпозиции обычно рассматривается в связи с законом Кулона, хотя здесь его логика такая же. Отметим, что эта логика была известна еще Ньютону, который на основе принципа суперпозиции доказал справедливость соотношения (13.1) для неточечных, но сферически симметричных масс.


