ГЛАВА 13. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Важно подчеркнуть, что изложенная выше процедура не является только «словесной». В математическом анализе разработаны методы выполнения такого суммирования (основы этих методов были разработаны Ньютоном именно при решении задачи о взаимодействии неточечных тел). Владение этими методами не входит в программу школьного курса; школьник должен только понимать идею такого суммирования и уметь его выполнить в тех ситуациях, когда суммирование выполняется «словами» с использованием тех или иных соображений симметрии.
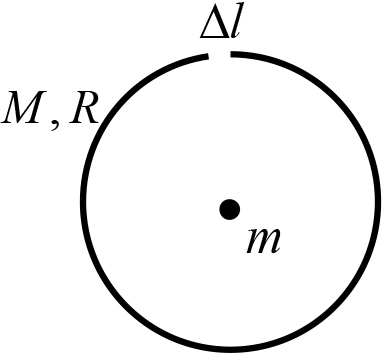
Рис. 13.2
Пример 13.4. Точечное тело массой m помещают в центр кольца массой M и радиусом R. Затем из кольца удаляют маленький кусочек длиной ![]() . Найти силу, действующую на точечное тело, со стороны остатка кольца (рис. 13.2).
. Найти силу, действующую на точечное тело, со стороны остатка кольца (рис. 13.2).
Решение. Если бы кольцо было целым, сила была бы равна нулю, Действительно, для нахождения силы на основе описанной выше процедуры кольцо необходимо разбить на малые части, найти силу, действующую на тело со стороны каждой части, просуммировать найденные вектора. Но благодаря симметрии кольца, для каждой его малой части существует противоположная часть, имеющая ту же массу и находящаяся на том же расстоянии. Поэтому суммарная сила и будет равна нулю (рис. 13.3, на котором показаны две компенсирующие друг друга силы ![]() и
и ![]() ).
).
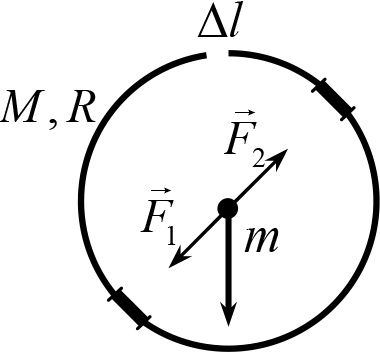
Рис. 13.3
Отсюда сразу следует метод нахождения силы в случае кольца с вырезанным элементом: силы, действующие на тело со стороны всех элементов кольца силы будут компенсировать друг друга за исключением силы, действующей на точечное тело со стороны элемента, противоположного удаленному. Таким образом, сила, действующая на тело со стороны всего кольца, равна силе, действующей только со стороны этого элемента. Вектор суммарной силы выделен на рис. 13.3. жирным.


