ГЛАВА 14. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
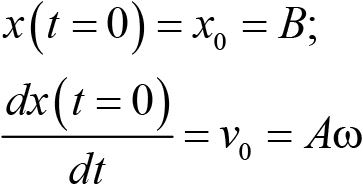
и A = ν0/ω, B = x0.
Величина ![]() в выражениях (14.4)–(14.7) называется круговой частотой колебаний. Эта величина связана с периодом колебаний. Действительно, поскольку период тригонометрических функций равен 2π, то значения координаты и скорости тела точно повторяются через такие интервалы времени, когда аргумент синуса или косинуса изменяется на 2πn (n — целое число). Очевидно, что минимальный интервал времени, через который повторяется значение координаты — период колебаний — равен
в выражениях (14.4)–(14.7) называется круговой частотой колебаний. Эта величина связана с периодом колебаний. Действительно, поскольку период тригонометрических функций равен 2π, то значения координаты и скорости тела точно повторяются через такие интервалы времени, когда аргумент синуса или косинуса изменяется на 2πn (n — целое число). Очевидно, что минимальный интервал времени, через который повторяется значение координаты — период колебаний — равен
Связь круговой частоты и периода колебаний (14.8) очень похожа на связь угловой скорости вращающегося тела и периода колебаний (12.6). Эта «похожесть» неслучайна. Дело в том, что если посмотреть на вращающееся тело «сбоку», то его движение будет казаться колебанием, причем период вращения будет равен периоду колебаний, а угловая скорость вращения будет совпадать с круговой частотой колебаний. Отсюда и связь формул (14.8) и (12.6).
Выражения (14.4)—(14.6) представляют собой зависимости координаты и скорости пружинного маятника от времени (так же как соотношения (4.2) для равноускоренного движения). Это значит, что t в этих выражениях — переменная, и подстановка любого значения времени в эти зависимости позволяет находить координату и скорость маятника в этот момент времени.


