ГЛАВА 14. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Нам же по условию нужно найти минимальный положительный корень. Поэтому из уравнения (14.10) получаем

Чтобы найти такие моменты времени , когда отклонение тела от положения равновесия равно половине амплитуды, воспользуемся первым из уравнений (14.9). Имеем

(знак ± появился потому, что по условию требуется исследовать отклонения от положения равновесия как в одну, так в другую сторону). Решая уравнение (14.11) и выбирая положительные корни, получаем две серии решений

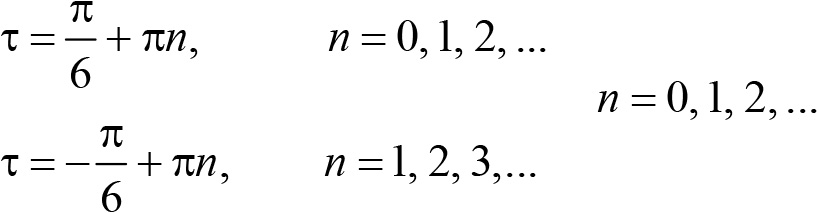
В школьном курсе физики рассматриваются две колебательных системы. Это, во-первых, рассмотренный выше пружинный маятник, а во-вторых, математический маятник. Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити. Название этой колебательной системы — «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. В случае малых отклонений от положения равновесия второй закон Ньютона для математического маятника можно привести к виду

где — угол отклонения маятника от положения равновесия; l — длина нити; g — ускорение свободного падения. Уравнение (14.12) совпадает с уравнением (14.3) для пружинного маятника, поэтому зависимость угла отклонения маятника от времени также будет даваться суммой тригонометрических функций