ГЛАВА 14. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
где круговая частота колебаний ω определяется длиной нити и ускорением свободного падения
Отсюда и из формулы (14.8) находим период колебаний математического маятника
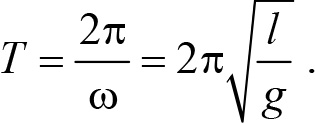
Важным методом описания колебаний является использование закона сохранения механической энергии. В пренебрежении силами трения или сопротивления механическая энергия маятника, которая представляет собой сумму кинетической и потенциальной, сохраняется. А поскольку кинетическая энергия тела зависит от его скорости, а потенциальная — от отклонения тела от положения равновесия, условие сохранения энергии позволяет связывать эти величины. Рассмотрим пример.
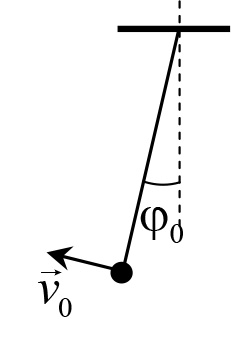
Рис. 14.2
Пример 14.2. Математическому маятнику длиной l, отклоненному на угол ![]() от положения равновесия, толчком сообщили скорость ν0 (рис. 14.2). На какой максимальный угол он отклонится? Какую максимальную скорость будет иметь? Какую долю от максимальной скорости будет составлять скорость маятника в тот момент, когда его отклонение от положения равновесия составляет половину амплитуды?
от положения равновесия, толчком сообщили скорость ν0 (рис. 14.2). На какой максимальный угол он отклонится? Какую максимальную скорость будет иметь? Какую долю от максимальной скорости будет составлять скорость маятника в тот момент, когда его отклонение от положения равновесия составляет половину амплитуды?
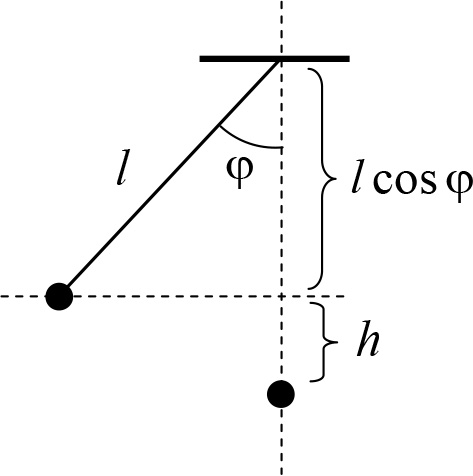
Рис. 14.3
Решение. Выберем за начало отсчета потенциальной энергии маятника
тот уровень, на котором он находится в положении равновесия. Тогда его потенциальная энергия при отклонении на некоторый угол ![]() определяется высотой подъема над этим уровнем h и может быть найдена геометрически (рис. 14.3). Из рисунка находим
определяется высотой подъема над этим уровнем h и может быть найдена геометрически (рис. 14.3). Из рисунка находим
![]()
(здесь использована известная тригонометрическая формула).


