ГЛАВА 14. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Для малых отклонений маятника синус угла можно заменить на сам угол. Поэтому потенциальная энергия математического маятника, отклоненного на малый угол , равна mglφ²/2. В результате для полной энергии математического маятника, совершающего малые колебания около положения равновесия, имеем

Используем теперь факт сохранения энергии маятника. В момент его отклонения на максимальный угол скорость маятника равна нулю. Поэтому

где — максимальный угол отклонения. Отсюда находим

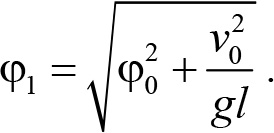
В момент прохождения положения равновесия равен нулю угол отклонения маятника, поэтому

где ν₁ — максимальная скорость маятника, откуда

Найдем теперь, какую долю от максимальной скорости составляет скорость маятника в тот момент, когда его отклонение от положения равновесия составляет половину амплитуды. Проще всего это сделать из следующих соображений. Поскольку потенциальная энергия маятника определяется выражением mglφ²/2, то в тот момент, когда его отклонение составляет половину амплитудного значения, потенциальная энергия маятника составляет одну четверть максимального значения. Поэтому из закона сохранения энергии следует, что кинетическая энергия маятника в этот момент составляет три четверти от ее максимального значения, а отношение скорости маятника к амплитудному значению скорости — .