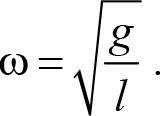ГЛАВА 14. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Существует еще один способ нахождения частоты колебаний — энергетический. Основную идею этого способа можно увидеть на примере пружинного маятника. С одной стороны, круговая частота колебаний равна . С другой, кинетическая энергия маятника есть mν²/2, потенциальная — kx²/2. Поэтому искать круговую частоту колебаний можно следующим образом. Нужно найти потенциальную энергию колебательной системы; она окажется пропорциональной квадрату ее отклонения от положения равновесия. Кинетическая энергия пропорциональна квадрату скорости. Квадратный корень из отношения коэффициента перед квадратом отклонения в потенциальной энергии к коэффициенту перед квадратом скорости в кинетической энергии и есть круговая частота колебаний. Рассмотрим пример.

Пример 14.5. Используя энергетические соображения, найти круговую частоту и период малых колебаний математического маятника. Длина маятника l.

Решение. Потенциальная энергия малых колебаний математического маятника найдена в примере 14.2

Кинетическая энергия маятника — mν²/2. Скорость маятника связана с его угловой скоростью dφ/dt через радиус окружности, по которой он движется (т.е. через длину нити)

Поэтому кинетическую энергию маятника K можно записать как

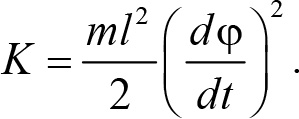
Отношение коэффициента перед ² в потенциальной энергии к коэффициенту перед (d/dt)² в кинетической и есть квадрат круговой частоты. В результате из (14.16), (14.17) находим круговую частоту :