ГЛАВА 14. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Поэтому нескомпенсированной будет сила притяжения муфты к кусочку стержня длиной 2Δx на правом конце стержня (на рис. 14.7 этот кусочек выделен). Найдем эту силу. Заряд этого кусочка ΔQ можно найти из очевидной пропорции

Отсюда получаем

Малость колебаний муфты означает малость смещения Δx по сравнению с длиной стержня, поэтому при вычислении силы взаимодействия муфты и участка стержня длиной 2Δx мы можем считать их точечными телами, расположенными на расстоянии l друг от друга, т.е. пренебречь как размерами тел, так и малым отличием расстояния между ними от l. Поэтому для силы их взаимодействия имеем

где k — постоянная закона Кулона. Из этой формулы видим, что возвращающая сила пропорциональна смещению, и потому согласно общим рецептам нахождения круговой частоты получаем

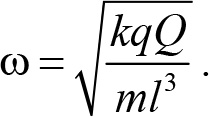
Рассмотренные выше примеры позволяют сформулировать следующие рекомендации по решению задач на колебательное движение. Все вопросы «по колебаниям», которые могут встретиться школьникам, можно разделить на три группы. Во-первых, это нахождение значений координаты или скорости колеблющегося тела при заданном значении скорости или координаты. Во-вторых, нахождение моментов времени, когда тело имеет то или иное значение координаты или скорости. И, в-третьих, нахождение частоты колебаний каких-либо колебательных систем.

Задачи первого типа проще всего решать, используя закон сохранения механической энергии.