ГЛАВА 2. ДВИЖЕНИЕ. ПУТЬ, ПЕРЕМЕЩЕНИЕ, СКОРОСТЬ. ДВИЖЕНИЕ С ПОСТОЯННОЙ СКОРОСТЬЮ
Для этого запишем формулы для пройденных телами до встречи путей, введя в них неизвестные величины, а затем составим уравнение, из которого эти неизвестные могут быть определены. Пусть, первое тело двигалось до встречи в течение времени τ. Тогда до встречи оно прошло расстояние l1 = v1τ. Второе тело двигалось до встречи такое же время (по условию тела начали движение одновременно) и, следовательно, прошло расстояние l2 = v2τ. Оба этих соотношения содержат по две неизвестных величины, и потому по отдельности не дают результата. Однако существует одно общее условие для двух тел – условие встречи. Поскольку в момент времени τ после начала движения тела встретились, то сумма расстояний, пройденных ими за это время, равна первоначальному расстоянию между ними (этот вывод иллюстрируется рис. 2.3)
Это и есть искомое уравнение, содержащее единственную неизвестную величину τ. Из формулы (2.3) находим время встречи
а затем из соотношения, связывающего пройденный путь, скорость и время для первого тела, находим расстояние от его начального положения до точки встречи тел
![]()
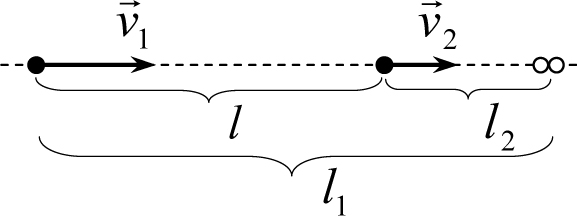
Рис. 2.4
Если бы тела двигались друг за другом, то разность расстояний, пройденных первым и вторым телом до встречи, равнялась бы первоначальному расстоянию между ними (рис. 2.4). То есть уравнение, из которого можно найти время встречи имеет вид (ср. с формулой (2.3))
![]()
или
![]()


