ГЛАВА 16. СТАТИКА
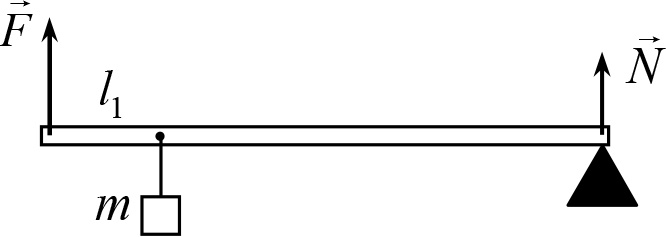
Рис. 16.3
В это уравнение будут входить те же самые три силы, и в результате мы получим систему уравнений, из которых искомая сила F и сила реакции опоры N могут быть определены. Но можно поступить и по-другому. Поскольку уравнение моментов (16.3) справедливо при любом выборе начала отсчета моментов, то можно эту точку выбрать так, чтобы момент одной из неизвестных сил был равен нулю. Тогда эта сила не войдет в уравнение моментов, и для определения неизвестной силы будет достаточно одного уравнения.
Итак, выберем начало отсчета моментов в точке контакта рычага и опоры. Тогда момент силы реакции равен нулю, момент силы ![]() равен −Fl, момент силы натяжения равен mg(l − l1). Поэтому уравнение моментов (16.3) для рычага дает
равен −Fl, момент силы натяжения равен mg(l − l1). Поэтому уравнение моментов (16.3) для рычага дает
![]()
Отсюда находим
![]()
В некоторых случаях в задачах статики приходится сталкиваться с вычислением моментов сил, у которых нет определенной точки приложения, и которые действуют на каждый элемент исследуемого тела. Такие силы принято называть распределенными в отличие от сил с определенной точкой приложения, которые в этом контексте называют сосредоточенными. Распределенными силами являются сила тяжести, трения, реакции опоры, действующие на протяженное твердое тело. Для вычисления момента распределенной силы — например, силы тяжести — нужно разбить тело на малые элементы, вычислить момент силы тяжести, действующей на каждый элемент, просуммировать полученные моменты. В результате суммарный момент силы тяжести оказывается таким же, как если бы полная сила тяжести была приложена к некоторой точке, которая называется центром тяжести тела.


