ГЛАВА 16. СТАТИКА
Можно доказать, что если тело обладает центральной симметрией (сфера, шар, прямоугольный параллелепипед), а элементарные силы, действующие на все элементы исследуемого тела, пропорциональны их массам и одинаково направлены (а только такие ситуации могут встречаться школьникам на ЕГЭ), то центр тяжести тела совпадает с его геометрическим центром. В этом случае для вычисления момента распределенной силы нужно равнодействующую распределенную силу приложить к геометрическому центру тела и вычислять момент этой силы так, как будто она является сосредоточенной. Единственное несимметричное тело, которое может встретиться в задачах школьного курса физики, — плоский треугольник. Его центр тяжести лежит в точке пересечения медиан. Рассмотрим следующий пример.
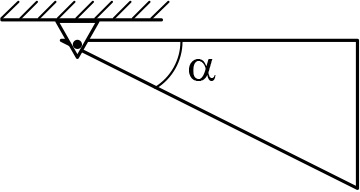
Рис. 16.4
Пример 16.2. Плоский прямоугольный треугольник массой и одним из острых углов α закреплен шарнирно за вершину этого угла и удерживается так, что один из его катетов параллелен поверхности земли (рис. 16.4). Какую минимальную силу нужно приложить для этого к треугольнику?
Решение. Чтобы треугольник был в равновесии момент искомой силы ![]() относительно шарнира должен быть равен по величине моменту силы тяжести. Поэтому сила F будет минимальна, если будет максимальным ее плечо относительно шарнира. Следовательно, внешнюю силу нужно приложить к точке треугольника, максимально удаленной от шарнира, и направить перпендикулярно отрезку, соединяющему эту точку с шарниром. То есть внешняя сила
относительно шарнира должен быть равен по величине моменту силы тяжести. Поэтому сила F будет минимальна, если будет максимальным ее плечо относительно шарнира. Следовательно, внешнюю силу нужно приложить к точке треугольника, максимально удаленной от шарнира, и направить перпендикулярно отрезку, соединяющему эту точку с шарниром. То есть внешняя сила ![]() должна быть приложена к вершине угла π/2 − α и направлена перпендикулярно гипотенузе (рис. 16.5).
должна быть приложена к вершине угла π/2 − α и направлена перпендикулярно гипотенузе (рис. 16.5).
Для того чтобы найти величину силы F воспользуемся вторым условием равновесия (16.3). Причем моменты сил будем вычислять относительно шарнира — это позволит сделать момент неизвестной силы реакции шарнира равным нулю.


