ГЛАВА 2. ДВИЖЕНИЕ. ПУТЬ, ПЕРЕМЕЩЕНИЕ, СКОРОСТЬ. ДВИЖЕНИЕ С ПОСТОЯННОЙ СКОРОСТЬЮ
Несмотря на то, что В.И. был одним из самых глубоких современных математиков (а, скорее всего, именно поэтому), он считал, что математика не должна существовать ради математики, а должна быть разделом естествознания, т.е. … частью физики. И что наиболее разумный ответ на вопрос «чему равно 3+2?» есть «5», а не «2+3, поскольку сложение коммутативно (перестановочно – авт.)». И что при решении математической задачи часто важнее основываться на здравом смысле и ее интуитивном понимании, чем на строгих доказательствах.
До последних дней своей жизни В.И. боролся с «реформой» школьного образования в нашей стране, с «реформой», в которой изучение наук и предметов фактически заменялось изучением экономики, права, менеджмента и иностранного языка. Боролся за то, чтобы наших детей в наших школах учили математике, физике, химии, литературе, географии, биологии, а не только «коммуникативной технологии в информатике».
Интересно, что наряду с математикой Арнольд сделал одно открытие в литературоведении, которым очень гордился: он нашел источник эпиграфа к «Евгению Онегину». В качестве эпиграфа к роману Пушкин взял переработанную фразу из французского романа в письмах «Опасные связи» Шодерло де Лакло.
Отметим, что по числу цитирований в научной литературе Арнольд занимает первое место среди всех советских и российских ученых.
Решение. На первый взгляд мало данных: ведь даны только времена, а скорости и расстояния не известны. Тем не менее, согласно рекомендованным выше принципам, давайте введем в задачу неизвестные величины и на основе соотношения «расстояние-время-скорость» для каждой старухи и для всех этапов движения (до и после встречи) составим уравнения, решения которых и позволят нам найти искомое время рассвета (время выхода старух).
Итак, пусть время выхода старух из дома (время рассвета) – t, скорости старух – v1 и v2. Тогда до встречи они пройдут расстояния v1t и v2t. После встречи первая старуха пройдет расстояние v1(16 − 12) = 4v1, а вторая – v2(21 − 12) = 9v2. Поскольку вторая старуха после встречи с первой пройдет то же самое расстояние, которое прошла первая до встречи и наоборот, то
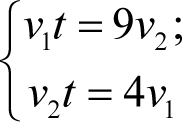
(здесь 9 и 4 – время в часах). Система уравнений (2.5) содержит три неизвестных величины, и потому не может быть решена относительно всех неизвестных. Но время рассвета найти можно.


