ГЛАВА 18. ГАЗОВЫЕ ЗАКОНЫ
Поэтому разность сил, действующих на поршень в конечном и начальном состояниях, равна силе тяжести дополнительного груза:
где m — масса груза. Выражая теперь давление ![]() из формулы (18.15) и подставляя его в (18.16), найдем
из формулы (18.15) и подставляя его в (18.16), найдем
![]()
До сих пор мы везде рассматривали однородный газ, т.е. такой газ все молекулы которого одинаковы. А если мы имеем смесь нескольких газов. Как в этом случае написать уравнение состояния, справедливы ли для такой смеси частные газовые законы и т.д.? Для установления уравнения состояния смеси газов можно рассуждать так. Как отмечалось выше, в уравнении состояния идеального газа полностью «пропадает» его индивидуальность — все определяется только количеством молекул газа и одна из форм уравнения состояния это подчеркивает
где N — число молекул газа, причем это уравнение имеет место независимо от того, какие у него молекулы (требуется только, чтобы газ был идеальным). Поэтому если газ представляет собой смесь разных газов, уравнение (8.17) также справедливо, но под N нужно понимать полное число молекул
где ![]() ,
, ![]() ,
, ![]() … – число молекул каждой компоненты, входящей в состав смеси. Уравнение (18.18) иногда записывают в другом виде. Так как
… – число молекул каждой компоненты, входящей в состав смеси. Уравнение (18.18) иногда записывают в другом виде. Так как
![]()
а ![]() k = R, то уравнение (18.18) можно переписать в виде
k = R, то уравнение (18.18) можно переписать в виде
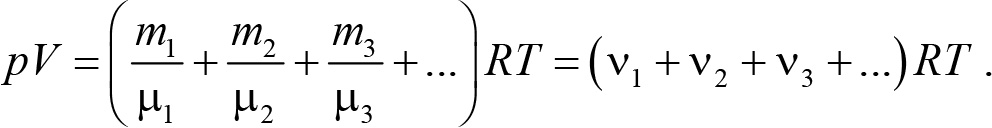
Здесь ![]() ,
, ![]() и
и ![]() — масса, молярная масса и количество вещества i-й компоненты смеси.
— масса, молярная масса и количество вещества i-й компоненты смеси.


