ГЛАВА 2. ДВИЖЕНИЕ. ПУТЬ, ПЕРЕМЕЩЕНИЕ, СКОРОСТЬ. ДВИЖЕНИЕ С ПОСТОЯННОЙ СКОРОСТЬЮ
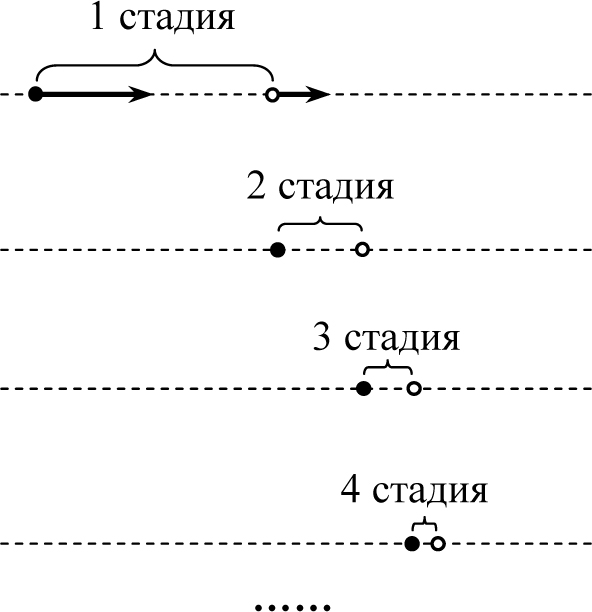
Рис. 2.5
Итак, каждая следующая стадия начинается, когда Ахиллес приходит в ту точку, где черепаха была в начале предыдущей. Ясно, что количество таких стадий, которые должны пройти Ахиллес и черепаха до встречи является бесконечно большим1, хотя каждая последующая и длится все меньше и меньше. Поэтому время, за которое Ахиллес догонит черепаху, равно сумме бесконечного количества слагаемых – интервалов времени, затраченных Ахиллесом на каждую стадию, то есть равно бесконечности. Таким образом, Ахиллес никогда не догонит черепаху. В чем ошибка этих рассуждений?

Зенон Элейский (ок. 490 г. до н.э. – ок. 430 г. до н.э.), древнегреческий математик и философ. Знаменит своими парадоксами, с помощью которых пытался доказать невозможность движения. Научные дискуссии, вызванные этими парадоксами, существенно углубили наше понимание таких фундаментальных понятий, как соотношение дискретного и непрерывного в природе, движения и покоя, единичного и множественного. На протяжении всей истории парадоксы Зенона являлись предметом внимания философов, логиков, математиков. Первым, кто подробно разобрал парадоксы Зенона (и от кого мы и знаем о Зеноне) был великий древнегреческий ученый Аристотель.
Решение. То, что эти рассуждения неправильны, ясно по результату. Ахиллес, имеющий скорость, большую скорости черепахи, догонит ее за время t = l / (v1 − v2), где l – первоначальное расстояние между Ахиллесом и черепахой (пример 2.1).
1 Ахиллес и черепаха предполагаются точечными.


