ГЛАВА 2. ДВИЖЕНИЕ. ПУТЬ, ПЕРЕМЕЩЕНИЕ, СКОРОСТЬ. ДВИЖЕНИЕ С ПОСТОЯННОЙ СКОРОСТЬЮ

Как следует из формулы (2.6), это время есть

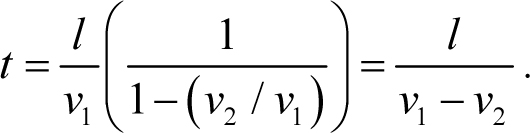
Мы получили то же время обгона Ахиллесом черепахи, что и при «обычном» способе решения (пример 2.1).

В заключение решения этой задачи отметим, что вычисление бесконечной суммы геометрической прогрессии (соотношение (2.6)) стало возможным после разработки математического анализа – раздела математики, оперирующего с бесконечно малыми и бесконечно большими величинами (именно потому, что древнегреческие математики не умели находить бесконечные суммы, и возник рассматриваемый парадокс). И то обстоятельство, что, суммируя бесконечную прогрессию, мы получили тот же ответ, что и при «обычном» способе решения свидетельствует о том, что не только «наглядные» разделы математики, такие как геометрия или арифметика, но и «абстрактный» математический анализ, имеют отношение к «реальной жизни».

Задачи для самостоятельного решения

2.1. Тело движется равномерно по окружности. Найти отношение пройденного пути к величине перемещения тела за четверть периода движения.

2.2. По периметру прямоугольника со сторонами 3 и 4 см маленький жук проходит за время 7 с. Какое время затратит жук, чтобы пройти с той же скоростью вдоль диагонали этого прямоугольника?

2.3. Одну треть пути от города А до города В автомобиль проехал с постоянной скоростью, затратив на это движение время t. Затем автомобиль увеличил скорость втрое и остаток пути проехал с этой новой скоростью. Какое время автомобиль затратил на весь путь?