ГЛАВА 3. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ

Итак, мы должны рассматривать движение любого тела глазами некоторого наблюдателя или, как говорят, в некоторой системе отсчета (под которой такой наблюдатель, имеющий линейку для измерения расстояний и часы для измерения интервалов времени, и подразумевается). При этом ряд кинематических характеристик тела – перемещение, пройденный путь, скорость – зависят от системы отсчета, в которой описывается движение тела, или, как говорят, являются относительными, и возникает вопрос о связи этих величин в разных системах отсчета. Рассмотрим следующий пример.

Пример 3.1. Поезд движется со скоростью v₁ = 60 км/ч. В поезде по направлению его движения перемещается человек со скоростью v₂ = 4 км/ч относительно поезда. Найти скорость человека относительно земли. Рассмотреть также случай, когда человек перемещается в поезде против его движения и общий случай произвольного направления вектора скорости человека в поезде.

Решение. Любой школьник сразу ответит на вопрос этой задчи – 64 км/ч. Но вопрос – а почему? – многих ставит в тупик. Давайте попробуем строго на него ответить.

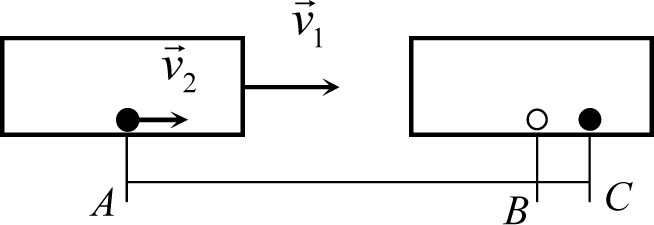
Рис. 3.1

Будем использовать определение скорости (предыдущую главу)

(3.1)

где Δt – произвольный малый интервал времени; Δ – вектор перемещения тела за этот интервал времени. Связь перемещений человека в системе отсчета, связанной с землей, и системе отсчета, связанной с поездом, легко увидеть из рис. 3.1. На этом рисунке изображены два положения поезда и человека – слева начальные, справа - спустя интервал времени Δt (человек изображен сплошным кружком, прозрачным кружком отмечена та точка поезда, в которой человек находился в начальный момент).