ГЛАВА 24. НАПРЯЖЕННОСТЬ И ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
где k - постоянная закона Кулона. В результате из (24.18)- (24.20) получим
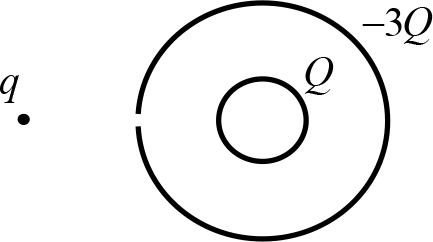
Рис. 24.10
Пример 24.6. Две закрепленные концентрические сферы радиусов R и 2R равномерно заряжены зарядами −3Q и Q (Q > 0 , рис. 24.10). В большой сфере сделано маленькое отверстие. На расстоянии 3R от центра сфер напротив отверстия удерживают точечный заряд q (q > 0), имеющий массу m. Заряд q отпускают. Достигнет ли он внутренней сферы, и если да, то какую скорость будет иметь?
Решение. Обсудим сначала «своими словами» постановку задачи. Заряд q притягивается к внешней сфере, но отталкивается от внутренней, причем первая сила больше последней, поскольку заряд внешней сферы больше. Поэтому пока заряд движется вне большой сферы, он движется в направлении общего центра сфер, разгоняясь. Когда же заряд проходит внутрь большой сферы, картина его движения меняется. Внешняя сфера на заряд перестает действовать (ведь заряд уже находится внутри нее!), а действует только внутренняя, причем эта сила - отталкивание. Но заряд уже набрал скорость, поэтому он продолжает двигаться в направлении центра, но его скорость уменьшается. И задача заключается в том, чтобы понять, долетит ли заряд до поверхности внутренней сферы или остановится раньше и повернет назад.
Применяем к движению заряда теорему об изменении кинетической энергии. Поскольку его начальная кинетическая энергия равна нулю, то он снова остановится, когда работа, совершенная над ним электрическим полем, будет равна нулю. Поэтому найдем работу, совершаемую полем над зарядом при его движении от начальной точки до поверхности внутренней сферы: если эта работа положительна, то заряд достигнет внутренней сферы (имея кинетическую энергию, равную этой работе), если работа поля отрицательна, заряд остановится раньше.
Для нахождения работы поля будем использовать формулу (24.15). Для этого найдем потенциалы начальной точки поля и точки, лежащей на поверхности внутренней сферы.


