ГЛАВА 3. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ
Векторный закон (3.7) включает в себя и оба частных случая, рассмотренных выше. Действительно, если векторы скорости поезда относительно земли ![]() 1 и скорости человека относительно поезда
1 и скорости человека относительно поезда ![]() 2 направлены одинаково, то, как это следует из правила векторного сложения, модуль вектора суммы равен сумме модулей векторов-слагаемых, а значит, величина скорости человека относительно земли равна сумме скорости поезда относительно земли и человека относительно поезда (формула (3.3)). Если векторы
2 направлены одинаково, то, как это следует из правила векторного сложения, модуль вектора суммы равен сумме модулей векторов-слагаемых, а значит, величина скорости человека относительно земли равна сумме скорости поезда относительно земли и человека относительно поезда (формула (3.3)). Если векторы ![]() 1 и
1 и ![]() 2 направлены противоположно, то модуль вектора суммы равен разности модулей векторовслагаемых (соотношение (3.4)).
2 направлены противоположно, то модуль вектора суммы равен разности модулей векторовслагаемых (соотношение (3.4)).
Несмотря на то, что формула (3.7) была получена для конкретной задачи (движение человека и поезда относительно земли), результат носит общий характер и может быть сформулирован так. Если тело по отношению к одному наблюдателю (в одной системе отсчета) имеет скорость  т.1, по отношению к другому наблюдателю (в другой системе отсчета) –
т.1, по отношению к другому наблюдателю (в другой системе отсчета) –  т.2, и второй наблюдатель движется по отношению к первому со скоростью
т.2, и второй наблюдатель движется по отношению к первому со скоростью  2.1 (скорость второй системы отсчета относительно первой), то векторы
2.1 (скорость второй системы отсчета относительно первой), то векторы  т.1,
т.1,  т.2 и
т.2 и  2.1 связаны соотношением
2.1 связаны соотношением
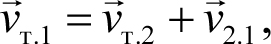 которое называется законом сложения скоростей. Геометрически формула (3.8) означает, что векторы скорости тела относительно первой системы отсчета
которое называется законом сложения скоростей. Геометрически формула (3.8) означает, что векторы скорости тела относительно первой системы отсчета  т.1, относительно второй системы отсчета
т.1, относительно второй системы отсчета  т.2 и вектор скорости второй системы относительно первой
т.2 и вектор скорости второй системы относительно первой  2.1 образуют треугольник (рис. 3.4), который называется треугольником сложения скоростей (или просто треугольником скоростей). А поскольку значение скорости тела – это модуль вектора его скорости, между величинами
2.1 образуют треугольник (рис. 3.4), который называется треугольником сложения скоростей (или просто треугольником скоростей). А поскольку значение скорости тела – это модуль вектора его скорости, между величинами  т.1,
т.1,  т.2 и
т.2 и  2.1 существуют такие же соотношения, как между сторонами треугольника в геометрии (в которые, конечно, входят и углы треугольника скоростей).
2.1 существуют такие же соотношения, как между сторонами треугольника в геометрии (в которые, конечно, входят и углы треугольника скоростей).
(3.8)
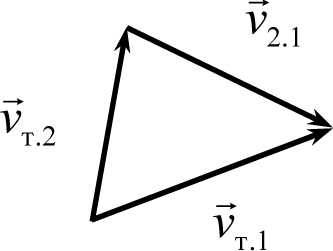
Рис. 3.4


