ГЛАВА 3. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ

Используя эти соотношения, можно найти неизвестные параметры треугольника сложения скоростей. Рассмотрим пример такого рода.

Пример 3.2. Поезд движется на север со скоростью v. Вектор скорости поезда относительно вертолета, пролетающего над поездом, направлен на северо-запад под углом α к меридиану и имеет модуль u. Найти скорость вертолета.

Решение. В условии задачи заданы векторы скорости одного и того же тела (поезда) относительно разных систем отсчета (земли и вертолета). А найти надо скорость вертолета относительно земли – т.е. одной системы отсчета относительно другой. Поскольку связь именно этих трех векторов дается законом сложения скоростей, то будем использовать его для решения.

Разберемся сначала, какие векторы нам заданы. Очевидно, что – это скорость поезда относительно земли = _п.з, 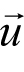– скорость поезда относительно вертолета 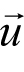= _п.в. По закону сложения скоростей имеем

(3.9)

где _в.з – скорость системы отсчета, связанной с вертолетом, относительно системы отсчета, связанной с землей, или, другими словами, скорость вертолета относительно земли. То есть та скорость, которую нам надо найти.

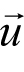
Поскольку закон сложения скоростей является векторным, из него не следует, что _в.з = v − u. Из закона сложения скоростей следует, что векторы , и _в.з связаны правилом векторного сложения, то есть образуют треугольник скоростей, причем значения

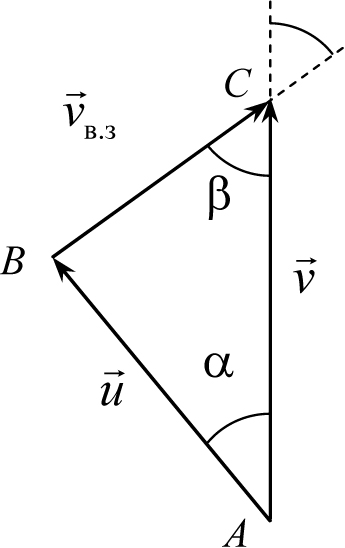
Рис. 3.5

скоростей равны длинам соответствующих сторон этого треугольника, а его углы - углам между направлениями скоростей. Поэтому для нахождения скорости вертолета относительно земли надо найти длину стороны треугольника сложения скоростей, отвечающую вектору _в.з, а для нахождения направления _в.з надо найти углы в треугольнике скоростей. Сделаем это геометрически.

Треугольник сложения скоростей, отвечающий рассматриваемой в задаче ситуации, изображен на рис. 3.5 (именно таким, как это показано на рисунке, должен быть вектор _в.з).