ГЛАВА 3. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ

На этом рисунке поезд изображен кружком и использовано принятое в географических картах расположение частей света: север – вверху, запад – слева и т.д.

По смыслу вектора скорости для треугольника скоростей ABC справедливы следующие соотношения: AB = u, AC = v, BC = v_в.з, ∠CAB = α. Поэтому по теореме косинусов имеем

Угол β между вектором _в.з и меридианом АС находим по теореме синусов

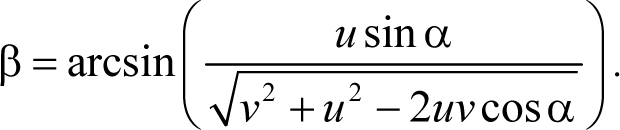
Благодаря тому, что закон сложения скоростей связывает друг с другом векторы скорости тела в разных системах отсчета, этот закон дает нам возможность выбрать для решения задачи такую систему отсчета, в которой рассматриваемое явление является наиболее простым. Действительно, может оказаться, что задача поставлена в такой системе отсчета, в которой анализ рассматриваемого явления не самый простой. Тогда можно с помощью закона сложения скоростей перейти в другую систему, в которой задача является более простой, решить ее, а затем (часто снова с помощью закона сложения скоростей) «вернуться» в первоначальную систему отсчета (последний шаг приходится делать не всегда). Давайте рассмотрим такой пример.

Пример 3.3. Два катера, идущие вниз по реке с разными скоростями, одновременно поравнялись с плывущим по течению плотом. Через одинаковое время катера повернули и с прежними относительно воды скоростями поплыли обратно. Какой из катеров дойдет до плота раньше?

Решение. Сразу и не скажешь. Ведь катера плывут с разными скоростями, которые, кроме того, различны при их движении вниз и вверх по течению. Плот также плывет по течению. Вот если бы это происходило в озере... Тогда, очевидно, катера вернулись бы назад одновременно. Действительно, за время движения вперед (обозначим это время t) катера проплыли бы расстояния l₁ = v₁t и l₂ = v₂t (v₁ и v₂ – скорости катеров в озере).