ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК. ЗАКОН ОМА ДЛЯ ОДНОРОДНОГО УЧАСТКА ЦЕПИ И ДЛЯ ЗАМКНУТОЙ ЦЕПИ. ЗАКОН ДЖОУЛЯ-ЛЕНЦА
Обычно закон Ома для участка цепи (27.3) рассматривают <арифметически>, т.е. все входящие в него величины считают положительными. Но в закон Ома можно вложить и <алгебраический> смысл. Действительно, напряжение на участке цепи 1-2 
может быть как положительным (если 
) и отрицательным (если 
). А поскольку положительные заряды текут по проводнику в направлении убывания потенциала (именно в этом направлении на них действуют силы со стороны поля), то закон Ома (27.3)
позволяет найти ток, текущий от точки 1 к точке 2. Если этот ток окажется отрицательным, то положительные заряды перемещаются в проводнике в противоположном направлении.
Для замкнутой электрической цепи, содержащей источник тока с ЭДС 
и внутренним сопротивлением r и внешнее сопротивление R (рис. 27.2), справедлив закон Ома для замкнутой цепи, позволяющий найти ток в этой электрической цепи
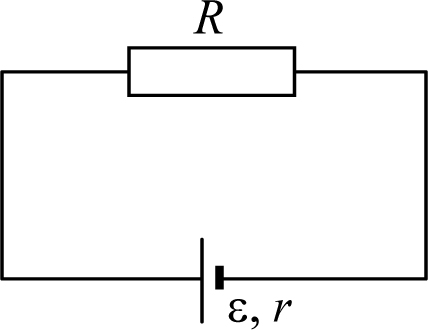
Рис. 27.2
На основании законов Ома для участка цепи и для замкнутой цепи можно рассчитать токи, напряжения и эквивалентные сопротивления не слишком сложных электрических цепей. Эквивалентным или общим сопротивлением любого комбинированного участка цепи называется отношение напряжения на этом участке к силе тока, протекающего через него
Рассмотрим применение закона Ома к двум наиболее важным соединениям элементов электрических цепей.
Последовательное соединение проводников. Пусть несколько проводников соединены последовательно. Приложим к этому участку цепи напряжение 
(рис.27.3).
