ГЛАВА 3. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ

Когда катера развернутся обратно, их скорости относительно земли будут равны (здесь мы опять используем закон сложения скоростей (3.10), но в случае противоположных направлений векторов _к.в и _в.з):

Так как теперь катера и плот движутся навстречу друг другу, катера – со скоростями (3.12), плот – со скоростью u, то катера подплывут к плоту через интервалы времени (см. пример 2.1)

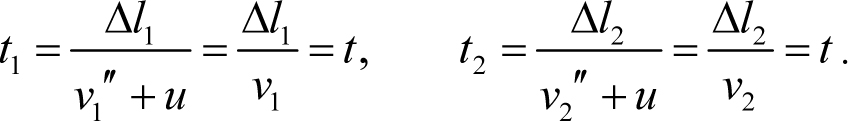
Таким образом, t₁ = t₂, и, следовательно, при решении задачи в системе отсчета, связанной с землей мы получаем тот же ответ, что и в системе отсчета, связанной с течением, однако в последнем случае для решения, нам, фактически, не понадобилось ни одной формулы.

В заключение обратим внимание на следующее интересное обстоятельство. Решение задачи в системе отсчета, связанной с водой, никак не меняется в случае, когда скорость одного или даже обоих катеров меньше скорости течения. Это значит, что и в этом случае катера приплывут к плоту одновременно, хотя картина их движения в системе отсчета, связанной с землей, будет совершенно другой. В этом случае при обратном движении катеров их будет сносить течением, и они будут двигаться по течению реки, но с меньшей, чем у плота скоростью. Поэтому правильнее сказать, что в этом случае плот будет догонять катера, причем догонит он оба катера одновременно.

Решенные задачи позволяют сформулировать основные идеи, связанные с законом сложения скоростей. Закон сложения скоростей дает связь между скоростями одного и того же тела по отношению к разным наблюдателям. Если в системе отсчета, связанной с одним наблюдателем, скорость тела равна _т.1, в системе отсчета, связанной с другим наблюдателем – _т.2, то векторы _т.1 и _т.2 связаны соотношением

где _2.1 – скорость второго наблюдателя по отношению к первому.

Закон сложения скоростей является векторным.