ГЛАВА 33. СВЕТОВЫЕ ЛУЧИ. ГЕОМЕТРИЧЕСКАЯ ОПТИКА. ЗАКОНЫ РАСПРОСТРАНЕНИЯ, ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА
Эйлер, Гаусс, Пуанкаре, другие менее крупные математики пытались, но не смогли этого сделать. В попытках доказать Великую теорему были созданы красивейшие математические теории и методы, а Теорема все стояла. Все это подталкивало к поиску доказательства и математиков и непрофессионалов — любителей математики. В результате Великая теорема Ферма обладает рекордом по числу придуманных неверных доказательств, который, наверное, никогда не будет побит. Но, пожалуй, самое удивительное заключается в том, что когда все математики уже смирились с мыслью, что теорема, скорее всего, неверна, и существует какой-то контрпример, Великая теорема Ферма все-таки была доказана. Доказательство было найдено уже в наше время американским математиком Эндрю Уайлсом. Его доказательство было опубликовано в 1995 г. — через 358 лет (!) после формулировки теоремы — и содержит 129 страниц печатного текста.
Давайте получим закон преломления света на основе принципа Ферма. Рассмотрим луч, проходящий из одной прозрачной среды в другую, и пусть его начало и конец фиксированы — точки S и S′ на рис. 33.11. Найдем по какому пути пройдет этот луч. Для этого рассмотрим все возможные лучи, начинающиеся в точке S и заканчивающиеся в точке S′. Очевидно, свет затратит на прохождение вдоль каждого луча следующее время
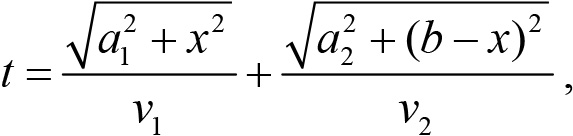
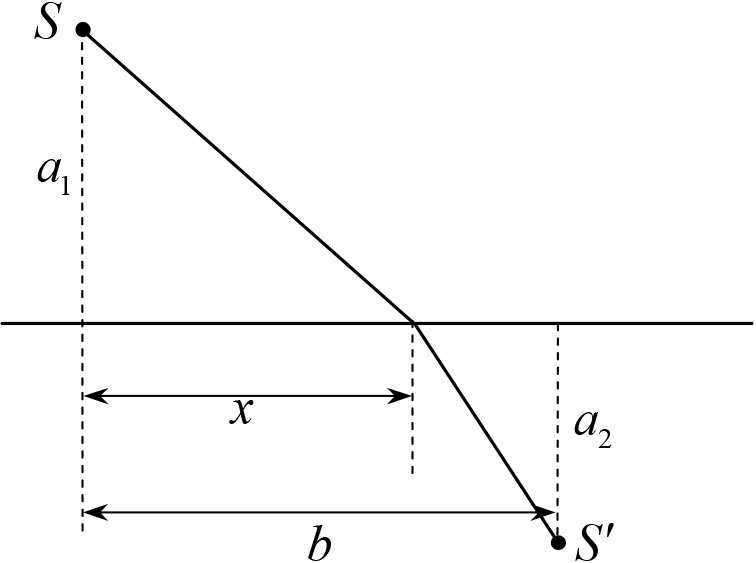
Рис. 33.11
где a1 и a2 — расстояние от точек S и S′ до границы между средами, x — расстояние от перпендикуляра, опущенного на границу между средами из точки S, до точки перехода луча из одной среды в другую, ν1 и ν2 — скорости распространения света в рассматриваемых средах. Принцип Ферма утверждает, что истинным будет тот луч, на прохождение по которой свет затрачивает наименьшее время.


