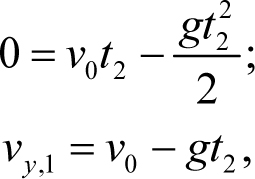ГЛАВА 4. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Для нахождения максимальной высоты подъема hmax и времени движения до этой точки t1 применим зависимости (4.4) к верхней точке траектории тела. То есть подставим в правую часть этих уравнений в качестве значения переменной t время движения до этой точки t1, которое пока нам неизвестно. Тогда первое из уравнений (4.4) даст нам значение y-координаты верхней точки траектории, второе – проекцию скорости тела на ось y в этот момент. Поскольку начало выбранной системы координат находится на поверхности земли, а ось y направлена вверх, то координата верхней точки равна максимальной высоте подъема y(t1) = hmax. Очевидно, скорость тела в верхней точке траектории равна нулю. Действительно, если бы проекция скорости тела в верхней точке на ось y была положительна, то тело в ней двигалось бы вверх и через небольшой промежуток времени поднялось бы еще выше (и, значит, рассматриваемая точка не является верхней). Если бы проекция скорости тела в этой точке была отрицательна, то тело в ней двигалось бы вниз, и, следовательно, чуть раньше находилось выше (и рассматриваемая точка снова не является верхней). Отсюда следует, что vy(t1) = 0. Поэтому зависимости (4.4), примененные к верхней точке траектории, дают
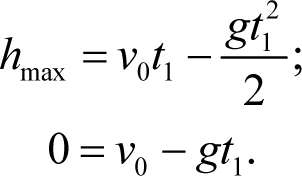
Из второго уравнения находим время подъема t1 = v0 / g. Подставляя его в первое уравнение, находим максимальную высоту подъема ![]() .
.
Для нахождения величин, относящихся к точке падения, подставим в зависимости (4.4) неизвестное полное время движения t2. Тогда левые части уравнений (4.4) дадут y-координату тела и проекцию его скорости на ось y в момент падения. Поскольку в момент падения y-координата тела равна нулю (напомним, что начало нашей системы координат находится на поверхности земли), то применение зависимостей (4.4) к моменту падения дает